099 2

196 X. Badanie przebiegu zmienności funkcji

asymptotą pionową krzywej y=f(x); natomiast gdy *->2-0, to /(x)-+-oo, a gdy _x -►2 + 0, to /(x)-» + oo, a więc prosta x = 2 jest też asymptotą pionową krzyw •

y-/M.    ^

Następnie badamy zachowanie sie funkcji f(x) w nieskończoności:

lim y= 1 i lim y = 1,

X~* ~ CO    X-* + co

co dowodzi, że prosta y- 1 jest dwustronną asymptotą poziomą krzywej. Układamy tabelkę przebiegu zmienności danej funkcji:

X	— 00	...		-2	...	0			2		+ 00
y	0	+	+ 00	+ 00	+	0	-	—co	—00	-	0
y	i		+ 00	— 00		0	\	— 00	+ co	\	1

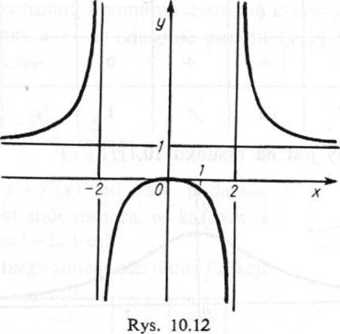
Wykres funkcji przedstawia rysunek 10.12.

Zadanie 10.14. Zbadać przebieg zmienności funkcji

x² —3

y=

x-2

Rozwiązanie. Funkcja jest określona dla x#2.

Po podzieleniu licznika przez mianownik możemy przedstawić funkcję w postać'

(1)

Obliczmy pochodną

y—x+2+

x —2

1    x²—4x+3 (x — 1) (x — 3)

(x —2)² (x — 2)² (x —2)²

Pochodna jest równa zeru przy x = 1 oraz x=3 i wówczas badana funkcja/(x) P^r®^f wartości /(1) = 2, /(3) = 6.

Widzimy dalej, że

lim /(x)=—oo i lim /(*)=+ oo,

x-*2 — 0    x-*2 + 0

więc prosta x = 2 jest asymptotą pionową krzywej (1).

Mówimy, że prosta y = ax+b, a 4= O, jest jednostronną (dwustronną) asymptotą ukośną krzywej, jeżeli zachodzi jedna (zachodzą obie) z następujących równości:

lim (f(x) — ax—b) = O lub lim (/(*)— ax-ó) = 0.

X~* + ao    - co

(10.410) Jeżeli funkcja y=/(x) daje się przedstawić w postaci y = ax+b+g(x), przy czym spełniony jest przynajmniej jeden z warunków.

lim g(x) = 0, lim g(x)=0,

X~* - oo    x-» + co

to prosta y = ax + b jest asymptotą ukośną krzywej y=f(x) (por. też str. 204).

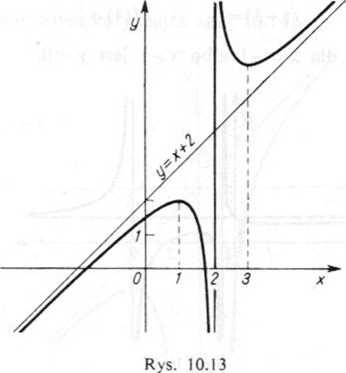
W tym przypadku dwustronną asymptotą ukośną jest prosta y = x + 2, gdyż

1 1

lim -= 0    i lim -= 0.

x~* — ao X 2    x~* + co X 2

Układamy tabelkę zmienności danej funkcji:

^----
*	— co		1		2			3		+ oo
	i	4*	0	—	— OO	— 00	—	0	+	1
y	— 00	z^1	2	\	— 00	+ 00		6	/*	+ oo

^kres

funkcji przedstawia rysunek 10.13.