098 2

194 X. Badanie przebiegu zmienności funkcji

Zadanie 10.11. Zbadać przebieg zmienności funkcji

2x —3

Rozwiązanie. Jest to tzw. funkcja homograficzna (iloraz dwóch funkcyj liniowy^ Funkcja jest określona, gdy jr+1^0, tzn. gdy x^-l.

Zbadajmy zachowanie się funkcji w otoczeniu punktu x = — 1. Gdy x-> —1 -0 (szukam granicy lewostronnej), to y-> + oo, a gdy x~* -1+0 (szukamy granicy prawostronnej^' to y-* — oo; w takim przypadku mówimy, że prosta x=-l jest asymptotą pionową krzywej y=f (x). Zauważmy bowiem, że gdy x= - 1-0, to odległość punktu (x,y) _Wy_ kresu funkcji y-f(x) od prostej x= —1 dąży do zera.

Zbadajmy granicę funkcji, gdy x wzrasta nieograniczenie:

2x —3

lim -=2

c-* — oo X 4" 1

2x —3

lim --— =2,

x~* + i© X “I" 1

a więc prosta ,y = 2 jest dwustronną asymptotą poziomą krzywej. Zauważmy bowiem, że zarówno gdy x->oo, jak i gdy x-> - co odległość punktu (x, y) wykresu funkcji y-f(x) od prostej y=2 dąży do zera.

Obliczamy pochodną

, 2(x + l)-(2x-3)    5

^V    (x + l)² (x + l)²'

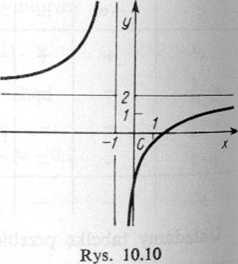
Dlax#-1 pochodna y'=f\x) jest stale dodatnia, a więc funkcja y = /(x) jest stale rosnąca, w każdym z przedziałów ( - oo, — 1) oraz (— 1, + oo).

Okładamy tabelkę przebiegu zmienności danej funkcji:

X	— OO		-1			+ co
y'	0	+	-rco	+ 00	+	0
y	2	/	+ 00	— 00		2

Wykres funkcji przedstawia rysunek 10.10.

Zadanie 10.12. Zbadać przebieg zmienności funkcji

1

Rozwiązanie. Funkcja jest określona dla wszystkich wartości x. Obliczmy pochodną

,    ~2x

0 j*^5t

'^V (l+x²)²

Pochodna przybiera wartość zerową, gdy x = 0. Dla x<0 jest dodatnia, a dla x>

„ina Obliczamy drugą pochodną _ujen>"^a-

^J    . r_v2

// /■> y = -2

(1 + x²)² —x -2(1 +x²) • 2x

2\4

d+*²)

2(3x² —1) (l+x²)³ ‘

Mianownik jest dodatni, a więc znak y" jest zgodny ze znakiem 3x² — 1. Gdy -i _v/3<x< '^\A ^<^^ruo^a pochodna /"(x) jest ujemna, więc krzywa y=f(x) jest wklęsła, a dla albo x>$j3 jest f"(x)>0, więc krzywa y=f(x) jest wypukła.

Poza tym zauważmy, że

1 1

lim -5=0 i lim -5=0,

x-*~ ooł "ł"X    x-* + aol+X

_c0 dowodzi, że oś Ox jest dwustronną asymptotą poziomą krzywej. Układamy tabelkę przebiegu zmienności danej funkcji:

Rys. 10.11

X	— OO		-Wi		0		łV3		+ 00
y"	0	+	0	-	-	-	0	+	0
/	0		+	+	0	-	-	-	0
y	0	/	i		1	\	i	\	0

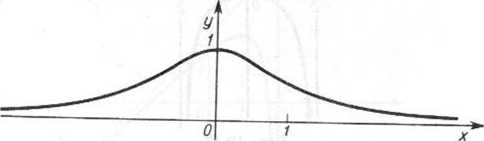
Wykres funkcji podany jest na rysunku 10.11.

Zadanie 10.13. Zbadać przebieg zmienności funkcji

..2

y=

x²—4

Rozwiązanie. Funkcja jest określona, gdy x²—4/0, tzn. gdy x#— 2 i x#2. Obliczając pochodną otrzymujemy

— 8x

y =

(x² —4)²

^obnie: jak w poprzednim zadaniu: dla x<0 mamy j'>0 i funkcja f(x) jest rosnąca, t, ***0 mamy /=0 i funkcja f(x) osiąga maksimum, dla x>0 mamy y'<0 i funkcja * jest malejąca.

gadajmy zachowanie się funkcji /(x) w otoczeniu punktów x——2 i x=2. Gdy "2~~0, to/(x)-> + oo, a gdy x-» —2 + 0, to /(*)-» — oo, a więc prosta x= —2 jest