101

200

X. Badanie przebiegu zmienności funkcji

Zadanie 10.17. Zbadać przebieg zmienności funkcji

O)    'TO

Rozwiązanie. Oznaczamy prawą stronę przez /(x) i rozkładamy mianownik

czynniki:

na

/(*)=

(x + l)(x-2)

Funkcja f(x) jest określona, gdy x# —1 i x#2.

Obliczamy pochodną /=/'(*); po zredukowaniu otrzymujemy

,    x²(x²—2x —6)

^y ~ (x + 1)²(x-2)² '

Punktami zerowymi pochodnej są: x, = l— \fl, x₂ = l + •Jl oraz x = 0 (pierwiastek podwójny).

Krzywa ma dwie asymptoty pionowe o równaniach x=-l i x=2.

Ponieważ licznik funkcji (1) jest stopnia wyższego niż mianownik, dzielimy ''^czn^ przez mianowmik:

3x + 2

a więc

x² —x —2

/(x) = x + l +

x² —x —2 3x +2

(x + l)(x-2)

Lrvvej

Z równości tej wnioskujemy, że prostay=*+ 1 jest dwustronna asvmptotą ukośną krzy k=/(x).    '    ,|j .

Ponieważ x = 0 jest podwójnym pierwiastkiem pochodnej, więc x = 0 jest ró^ pierwiastkiem (pojedynczym) drugiej pochodnej i łatwo wywnioskować, że jest to P^u^ przegięcia; w punkcie tym jest y' = 0, a więc krzywa jest styczna do osi odciętych-

L+ładamy tabelkę przebiegu zmienności danej funkcji:

X	—• OO		1-V7			-1		0			2		1 + V7	...	+ oo
/	i	+	0	-	— 00	— oo	-	0	-	— co	— 00	-	0	+	1
y	— 00	/	max	\	— 00	+ 00	\	0	\	— oo	4- oo	\	min	/	-f CO

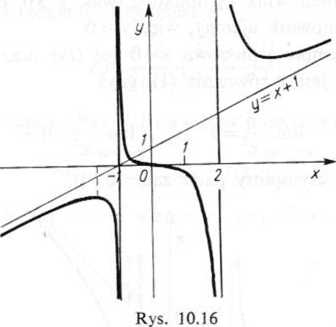
Wykres funkcji przedstawia rysunek 10.16.

Zadanie 10.18. Zbadać przebieg zmienności funkcji

11

7+7

Rozwiązanie. Funkcja jest określona tylko dla tych wartości, dla których wyrażenie id pierwiastkiem jest nieujemne, a więc dla — 1<x<1.

Po zróżniczkowaniu i redukcji otrzymujemy

-l

y =

(l+x)Vl— X²

W przedziale —1<x<1 jest zawsze y' <0, czyli funkcja y jest malejąca.

Obliczamy drugą pochodną. Po obliczeniu drugiej pochodnej otrzymujemy

1 —2x

y =

(l+x)(l-x)Vl-x²

Dla    jest y" = 0, dla x<$ jest y">0, a dla x>| jest p"<0, a więc x=\ jest to

punkt przegięcia krzywej y=/(x); w punkcie tym y = | _N/3.

Prosta x= —l jest asymptotą pionową, gdyż lim y= + co. Zauważmy, że

x-> -1 +o

lim y'= — oo i lim /= — oo.

x-* -1+0    x~* + 1—0

dowodzi, że w punkcie x = 1 styczna do krzywej y=f(x) jest równoległa do osi rzędnych, '^0ctl°dna bowiem, tj. współczynnik kątowy tg a stycznej, dąży do — oo, a wówczas *"4*+0.

biadamy tabelkę przebiegu zmienności danej funkcji:

X	-i		i		1
y"	4-co	+	0	-	• — 00
y	— 00	-	-	-	— 00
y	+ 00	\	W3	\	0

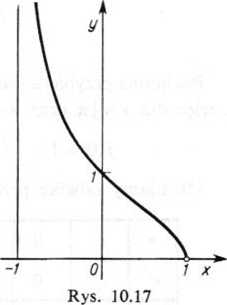
ykres funkcji podaje rysunek 10.17.

w.