096 2

190

X. Badanie przebiegu zmienności funkcji

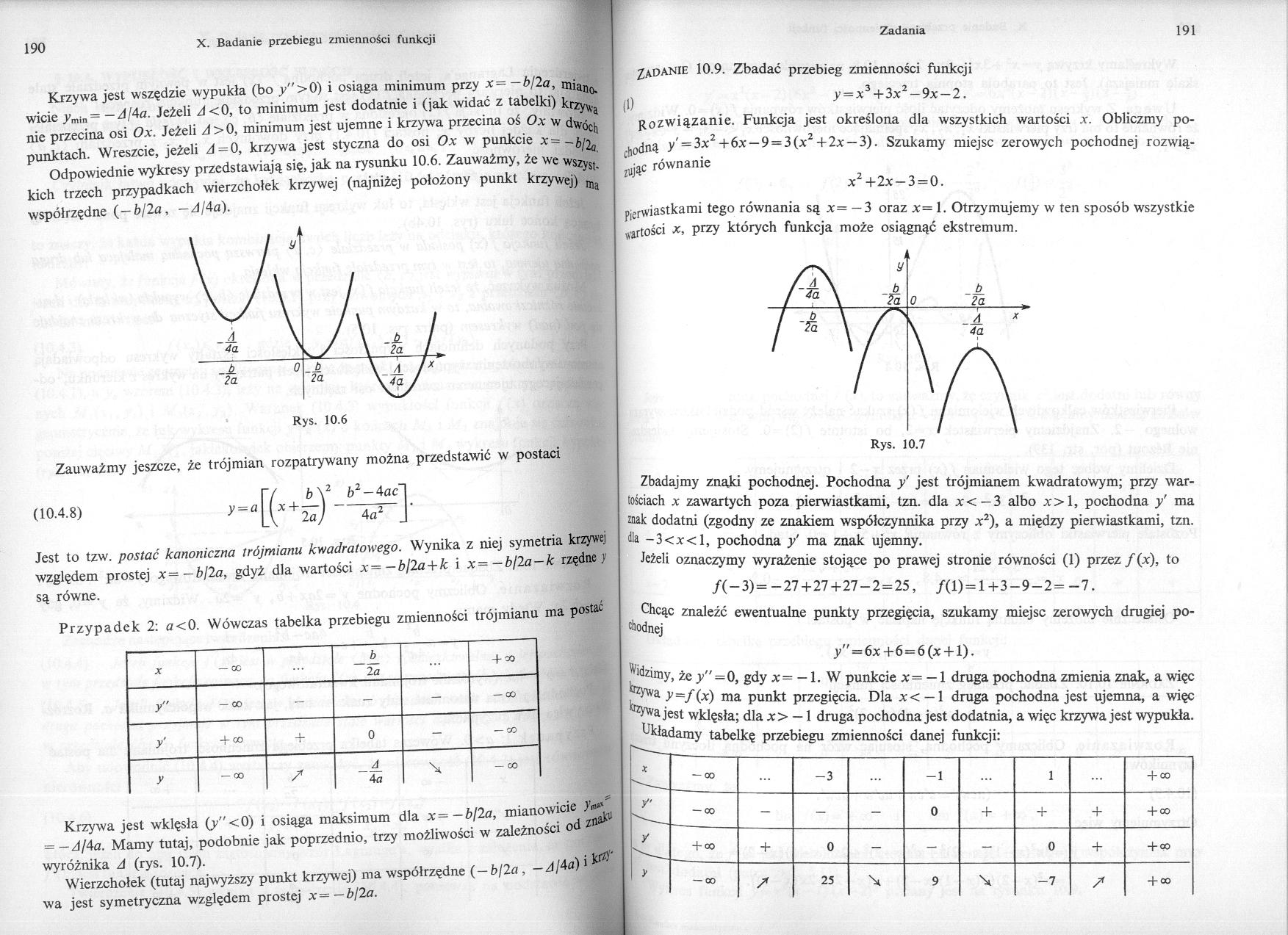
Krzywa jest wszędzie wypukła (bo _y">0) i osiąga minimum przy x=-b/2a, mia₀ wicie _y_min= — AjAa. Jeżeli A<0, to minimum jest dodatnie i (jak widać z tabelki) krzy^ nie przecina osi Ox. Jeżeli A>0, minimum jest ujemne i krzywa przecina oś Ox w dwó l punktach. Wreszcie, jeżeli A=0, krzywa jest styczna do osi Ox w punkcie x= -bjla Odpowiednie wykresy przedstawiają się, jak na rysunku 10.6. Zauważmy, że we wszy_s, kich trzech przypadkach wierzchołek krzywej (najniżej położony punkt krzywej) _ma współrzędne {—bjla, — A/Aa).

V b\² b²—Aacl ^{y =} a[[^{X +} 2^) —&-}•

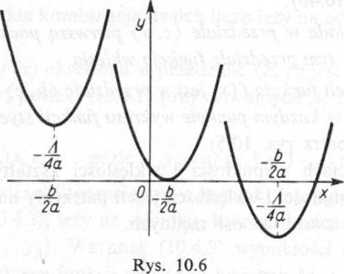
Zauważmy jeszcze, że trójmian rozpatrywany można przedstawić w postaci (10.4.8)

Jest to tzw. postać kanoniczna trójmianu kwadratowego. Wynika z niej symetria krzywej względem prostej x=—bl2a, gdyż dla wartości x=— b/2a + k i x= —bl2a — k rzędne.) są równe.

Przypadek 2: a<0. Wówczas tabelka przebiegu zmienności trójmianu ma postać

X	— oc		b 2 a	...	+»
y"	— 00	-	■	-	— 00
y'	-fco	+	0	-	— co
y	— 00	/	_4_ 4a	\	— co

Krzywa jest wklęsła (/'<0) i osiąga maksimum dla x= —bj2a, mianowicie = — AlAa. Mamy tutaj, podobnie jak poprzednio, trzy możliwości w zależności od Z wyróżnika A (rys. 10.7).    .

Wierzchołek (tutaj najwyższy punkt krzywej) ma współrzędne ( — b/2a, —AjAa)¹ wa jest symetryczna względem prostej x——b/2a.

Zadanie 10.9. Zbadać przebieg zmienności funkcji

y = x³+3x² —9x —2.

(0

Rozwiązanie. Funkcja jest określona dla wszystkich wartości .v. Obliczmy po-bodną y' = 3x²+6x —9 = 3(x²+2x —3). Szukamy miejsc zerowych pochodnej rozwiązać równanie

x² +2x —3=0.

powiastkami tego równania są x= —3 oraz x= 1. Otrzymujemy w ten sposób wszystkie wartości x, przy których funkcja może osiągnąć ekstremum.

Rys. 10.7

Zbadajmy znaki pochodnej. Pochodna y' jest trójmianem kwadratowym; przy wartościach x zawartych poza pierwiastkami, tzn. dla x<-3 albo x>l, pochodna y' ma mak dodatni (zgodny ze znakiem współczynnika przy x²), a między pierwiastkami, tzn. dla -3<x<l, pochodna y' ma znak ujemny.

Jeżeli oznaczymy wyrażenie stojące po prawej stronie równości (1) przez /(x), to

/(-3)=-27+27+27-2 = 25,    /(1) = 1+3-9-2= -7.

Chcąc znaleźć ewentualne punkty przegięcia, szukamy miejsc zerowych drugiej pochodnej

y" = 6x+6=6(x + l).

WiH ‘

‘cizimy, że y"=0, gdy x= — 1. W punkcie x= — 1 druga pochodna zmienia znak, a więc y =/ (x) ma punkt przegięcia. Dla x< —1 druga pochodna jest ujemna, a więc jest wklęsła; dla x> — 1 druga pochodna jest dodatnia, a więc krzywa jest wypukła.

^---
X	— 00		-3		-1		1	...	+ co
r	— oo	-	-	-	0	+	+	+	+ CO
y	+ 00	+	0	-	-	-	0	+	+ oo
y	— 00		25	\	9		-7	/	+ CO

Układamy tabelkę przebiegu zmienności danej funkcji: