108 2

214 X. Badanie przebiegu zmienności funkcji

gdzie x jest to odległość danego punktu belki od punktu jej umocowania (w cm), p _ . obciążająca belkę (w kg), / - długość belki (w cm), E, J - wielkości stałe dla danej bel),⁴ Znaleźć maksymalne ugięcie belki, gdy /=20 cm, P=600 kg.

Rozwiązanie. Badamy funkcję y w przedziale 0<x</. Obliczamy pochodną

^(I*²-/x).

dx ej^K2

Wartość pochodnej równa się zeru dla x=0 i x=2/, a zatem poza przedziałem 0 <*</ W badanym przez nas przedziale pochodna jest stale ujemna. Funkcja maleje od 0 do wartości

EJ

EJ

Maksymalne ugięcie w tym przypadku wynosi

i

3

600

U

•8000=

1600000 “ EJ

Zadanie 10.37. Wskaźnik wytrzymałości W belki prostokątnej, poziomo leżącej, wyraża się wzorem W=\xy², gdzie x jest szerokością, y — wysokością przekroju belki. Jak wyciąć z pnia mającego kształt walca, którego podstawa ma średnicę równą a, belkę prostokątną o największym wskaźniku wytrzymałości (rys. 10.32).

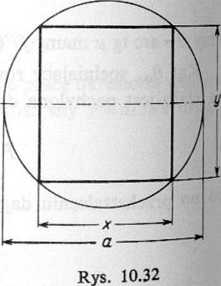
Rozwiązanie. Z twierdzenia Pitagorasa otrzymujemy y²=a² — x², więc

W= | (a²x-x³), gdzie 0<x<a.

Obliczamy, przy jakich wartościach funkcja może osiągać ekstremum. Mamy

dW

dx

dW

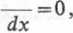
Ua²-3x²),

skąd

gdy

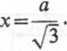
Przy tej wartości x mamy d² WJdx² < 0, a więc funkcja W(x) osiąga maksimum.

Zadanie 10.38. Wydajność tlenku azotu NO z mieszaniny a % tlenu i (100-<0 /° azotu w temperaturze 1600°C i pod ciśnieniem normalnym określa wzór

x = y/Ka (100-a)-25K,

gdzie K jest stałą równowagi reakcji dla danej temperatury i danego ciśnienia. Oblicz) ’ przy jakiej procentowej zawartości tlenu a % w mieszaninie wydajność tlenku az NO będzie maksymalna.

Rozwiązanie. Obliczamy pochodną

dx_ K(m-2a) da 2\l Ka(lOO—a)

przyrównując pochodną do zera otrzymujemy a = 50%.

Zadanie 10.39. Jasność I w punkcie odległym o r od źródła światła wyraża się wzorem l~k!r², gdzie k jest parametrem zależnym od wysyłanego strumienia światła. W punktach A i B znajdują się dwie różne żarówki, odległe od siebie o odcinek d (rys. 10.33). Żarówka A daje w punkcie B jasność a, a żarówka B daje w punkcie A jasność b. Wykazać, że jeżeli M jest punktem odcinka AB o jasności minimalnej, to AM: MB=\]a : IJb.

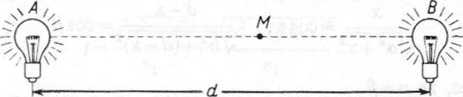
Rys. 10.33

Rozwiązanie. Wyznaczamy parametry k żarówek:

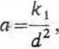
więc ki=ad²,

oraz

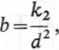
więc k₂ = bd².

Niech AM=x; wówczas MB=d-x. Jasność w punkcie M wynosi

_adf bd² x² (d—x)²

Wyznaczamy punkt o minimalnej jasności:

dl ad² bd² ~dx 2

skąd

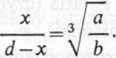
dl

—=°.    gdy

dx

^Stąd otrzymujemy AM : MB=Xfaib.

Udanie 10.40. Odcinki MA=ci i NB = b (rys. 10.34) przedstawiają odpowiednio °kości latarń wznoszących się nad jeziorem. Odległość między latarniami wynosi d. ^^0rnień z latarni A odbija się od gładkiej powierzchni jeziora w punkcie L i dobiega Punktu B tak, że jego droga AL + LB jest najmniejsza. Wykazać, że kąt %.ALM = p ^Sl równy kątowi A:BLN=a.