104 2

206 X. Badanie przebiegu zmienności funkcji

Dla x = 0 z równości (2) otrzymujemy y = 0; również dla x=2R jest y = 0. Układamy tabelkę przebiegu zmienności funkcji (2):

X	0	...	5*	...	2 R
/	+	+	0	-	-
y	0	/		\	0

Objętość kuli wynosi |nR³. Dzieląc maksymalną objętość stożka przez objętość kuli otrzymujemy co oznacza, że stożek obrotowy o największej objętości wpj_sanv w kulę zajmuje (a więc mniej niż i) objętości kuli.

Zadanie 10.24. Jakie wymiary powinno mieć naczynie kształtu otwartego walca obrotowego o danej pojemności V, gdy przy danej grubości ścianek a chcemy zużyć jak najmniej materiału?

Rozwiązanie. Niech y oznacza ilość materiału zużytego na budowę walca (wyrażoną w takich samych jednostkach, oczywiście sześciennych, w jakich wyrażone są wielkości V i a).

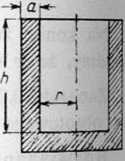
Rys. 10.22

Pojemność naczynia (rys, 10.22) wynosi V=nr²h. Ilość materiału y jest różnicą między objętością walca o promieniu podstawy r+a i wysokości h + a a daną objętością V, a więc

(1)    y = n(r + a)²(h+a) — nr²h.

Ze związku V-nr²h wyznaczamy h= V(nr² i podstawiamy do (1).

Otrzymujemy

y = 7t(r + a)²

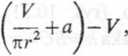
gdzie y jest funkcją zmiennego promienia r (wielkości a i V są dane).

Aby wyznaczyć ekstremum tej funkcji, obliczamy pochodną i przyrównujemy ją ^1,0 zera:

= 7t-2 (r + a)

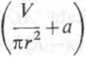
+ rt(r + a)²

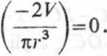
równan'^£

Następnie dzielimy przez 2n(r + a) i po wykonaniu mnożenia i redukcji mamy

aV

(2)    a--3=0,

itr

skąd z łatwością otrzymujemy, że pochodna równa się zeru, gdy r=\f K/rt. Łatwo ^sP^ra dzamy, że wysokość walca h jest wówczas równa promieniowi r:

ponieważ znak y' jest taki sam, jak znak wyrażenia stojącego po lewej stronie rów-•iści (2), więc J^est widoczne, że dla r<X/vin pochodna jest ujemna, a dla r> VV/n po-•_uodna jest dodatnia, czyli dla r= V Vfn funkcja osiąga minimum.

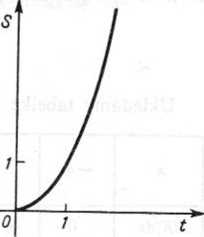
Zadanie 10.25. Droga przebyta przez ciało swobodnie spadające (przy pominięciu _rU powietrza) wyraża się wzorem

S=V₀ł+jgt²,

^ie ^v° ^oznacza prędkość początkową (w momencie /=0), oznacza przyśpieszenie grawitacyjne, ar- czas. Wyznacie prędkość ruchu ds\dt i sporządzić wykres funkcji

!=/(')•

Rozwiązanie. Obliczamy prędkość ruchu jako pochodną

ds

— = ^vo+gt.    Rys. _10-23

Wykres funkcji s=f(t) dla r^O jest to gałąź paraboli (rys. 10.23), do której styczna w punkcie f=0 ma współczynnik kątowy v₀.

Zadanie 10.26. Pole elektryczne wytworzone jest przez dwa ładunki punktowe +e i -2e, które są od siebie oddalone o odcinek d. Sporządzić wykres natężenia K pola elektrycznego wzdłuż prostej przechodzącej przez te ładunki.

+e    x    +2e

—*■

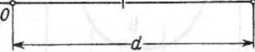
x

Rys. 10.24

Rozwiązanie. Obierzmy układ współrzędnych jak na rysunku 10.24. Zgodnie z pra-"^etn Coulomba natężenie K wyraża się wzorem

^^Z'^e ^ jest to współczynnik zależny od wyboru jednostek. Funkcja ta jest określona przy

tystkich wartościach x z wyjątkiem 0 i d. Granice funkcji w punktach nieciągłości

wynoszą;

lim K(x)=+ oo, lim K(x)= + oo, *•*-<>    *- + 0

lun K \x)= +oo,

x-*d — 0

x->d + 0

P^roste x=0 i x—d są asymptotami pionowymi. Ponadto zauważmy, że

lim K(x)= lim K(x)=0,

^iv,ięc

x~* - co    *-> + 00

prosta K= 0 jest dwustronną asymptotą poziomą.