img485

Przeprowadzimy badanie przebiegu zmienności funkcji f(x) - x +

x - 2

Następnie, korzystając z otrzymanego wykresu, znajdziemy wykres funkcji

= m (m e R).

4

x- 2

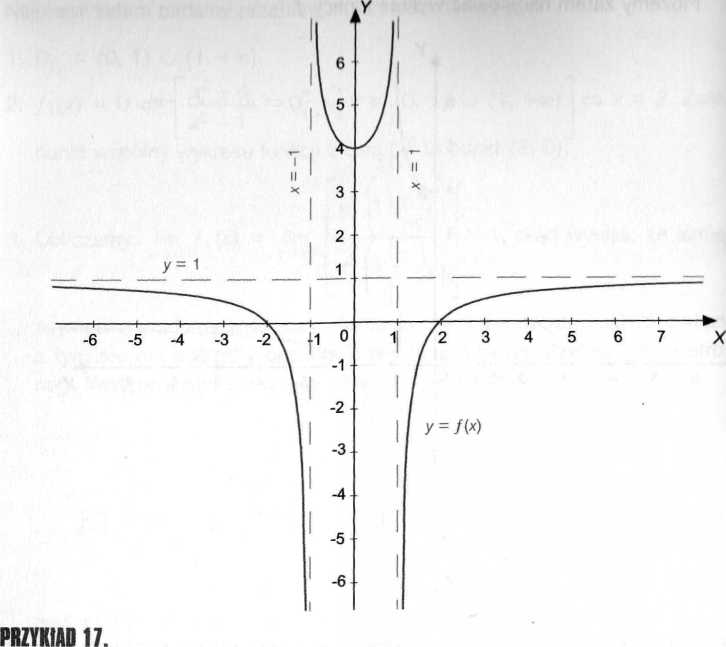
y ⁼ 9i^m)< będącej liczbą rozwiązań równania x +

1 ■ Df = ( go, 2) u (2, +oo).

2.    Funkcja nie jest okresowa. Nie jest ani parzysta, ani nieparzysta (uzasadnij).

3.    Wyznaczamy miejsca zerowe funkcji:

x² - 2x + 4

\

- O a x e D

oxe0.

^v    y

Zatem brak miejsc zerowych i, co za tym idzie, brak punktów wspólnych wykresu z osią OX. Ponieważ /(O) = -2, więc punkt wspólny wykresu z osią OY to punkt (O, -2).

asymptoty poziomej wykresu. Mamy dalej, Hm /(x) = -oo i, podobnie, linr. /(x) = +oo, skąd wynika, że prosta x = 2 jest asymptotą pionową wykresu funkcji.

Zbadamy istnienie asymptoty ukośnej. Mamy:

lim = lim

x-»±oo X X-»±oo

1 +

x(x-2)

= 1, skąd a = 1;

x -2

4, Obliczamy: lim f(x) = lim x +

= -oo, lim /(x) = +oo. Brak więc

x->+®

oraz

lim f/(x) - ax] = lim

X-»±00 ¹    x->±00

x- 2

O, skąd b = O.

Istnieje więc asymptota ukośna wykresu o równaniu y = x.

5. Obliczamy pochodną

x +

Y

x- 2

= 1 -

4

x² - 4x

(x - 2)² (x - 2)=

. Widzimy, że

Df = Df. Dalej otrzymujemy

/'(x) = O (x² - 4x = O a x e Df) <=> (x = O v x = 4), f(x) > O « (x² - 4x > O a x e Df) <=> x e (-oo, O) U (4, +oo), f'(x) <0ox£ (O, 2) u (2, 4).

6. Wstawiamy rezultaty obliczeń do tabelki:

/'(*)

m

(-00, 0)	0	(0, 2)	2	(2, 4)	4	(4,+oo)
+	0	-	X	-	0	+
* -oo	maksimum lokalne -2	-00	X	+00	minimum lokalne 6	+oo *

HH

7. Teraz możemy już naszkicować wykres: