097 2

192 X. Badanie przebiegu zmienności funkcji

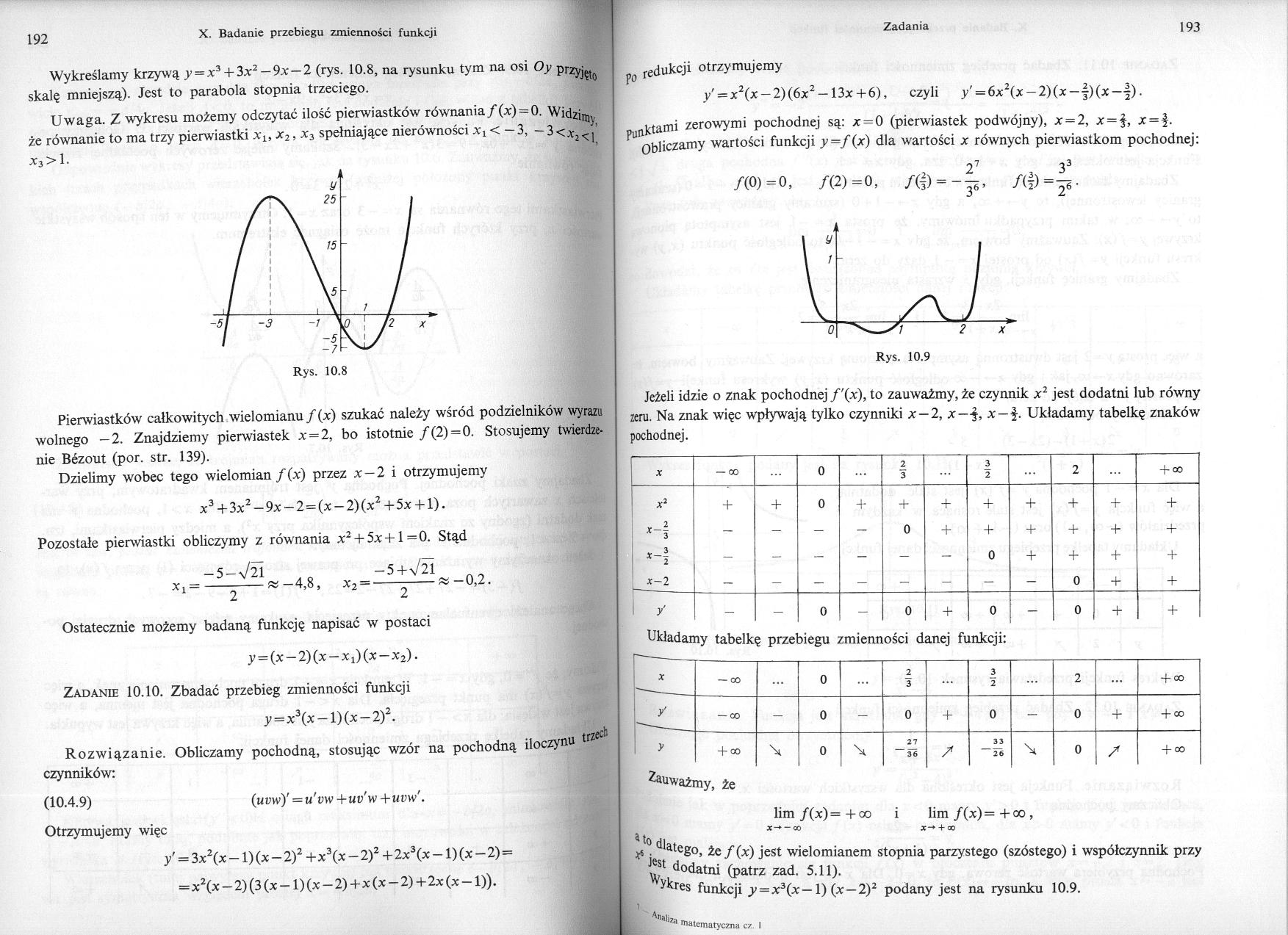
Wykreślamy krzywą y = x³ + 3x² —9x — 2 (rys. 10.8, na rysunku tym na osi Oy przyjęć skalę mniejszą). Jest to parabola stopnia trzeciego.

Uwaga. Z wykresu możemy odczytać ilość pierwiastków równania/(x) = 0. Widzie, że równanie to ma trzy pierwiastki x_u x₂, x₃ spełniające nierówności Ay < -3, - 3<_Xj<]’

x₃ > 1.

Pierwiastków całkowitych wielomianu /(a) szukać należy wśród podzielników wyrazu wolnego —2. Znajdziemy pierwiastek a = 2, bo istotnie /(2) =0. Stosujemy twierdzenie Bezout (por. str. 139).

Dzielimy wobec tego wielomian /(a) przez a—2 i otrzymujemy x³ +3a² —9a —2 = (x —2)(x² +5x + l).

Pozostałe pierwiastki obliczymy z równania x² + 5x + l=0. Stąd

-5-y/ll    -5+V21

x, =-« — 4,8, x₂ =-«— 0,2.

2 2

Ostatecznie możemy badaną funkcję napisać w postaci

y=(x-2)(x-A₁)(x-x₂).

Zadanie 10.10. Zbadać przebieg zmienności funkcji

y=x³(x —l)(x —2)².

Rozwiązanie. Obliczamy pochodną, stosując wzór na pochodną iloczynu czynników:

(10.4.9)    (uvw)'=u'vw+uv'w+uvw

Otrzymujemy więc

y' = 3x²(x — 1)(x — 2)² +x³(x - 2)² +2a³(x -1) (x -2) =

= x²(x — 2) (3 (x — 1) ( a — 2) + a (x — 2) + 2x (a —1)).

_po redukcji otrzymujemy

y' = x²(x- 2)(6x² —13x+6), czyli    y' = 6x²(x-2)(x — |)(x — |).

mmi zerowymi pochodnej są: x = 0 (pierwiastek podwójny), x = 2, x = $, x = \. Obliczamy wartości funkcji y=f(x) dla wartości x równych pierwiastkom pochodnej:

/(O) =o, /(2) = o,    =    r(D=|J-

Jeżeli idzie o znak pochodnej f'{x), to zauważmy, że czynnik x² jest dodatni lub równy zeru. Na znak więc wpływają tylko czynniki x-2, x--§, x-\. Układamy tabelkę znaków pochodnej.

X	— 00		0		2 3		3 2		2		-f co
X^2	+	+	0	+	+	+	+	+	+	+	+
*-f	-	-	-	-	0	+	+	+	+	+	~r
H	-	-	-	-	-	-	0	+	+	+	+
_ x—2	-	-	—	—	—	-	—	—	0	4-	+
y	-	-	0	-	0	+	0	-	0	+	+

Układamy tabelkę przebiegu zmienności danej funkcji:

X	— 00		0		2 3	...	3 2		2	...	+ oo
y	— oo	-	0	-	0	+	0	-	0	+	+ 00
y	+ co	\	0	\	27 36	/	33 26	\	0	/	+ oo

Zważmy, że

⁵1₀

lim /(x) = +oo i

X~* ~ CO

lim /(x) = +oo,

X~* + 00

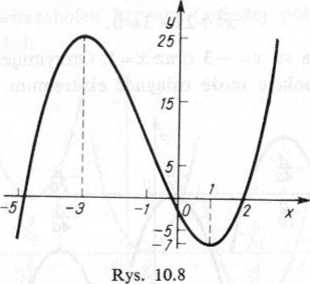
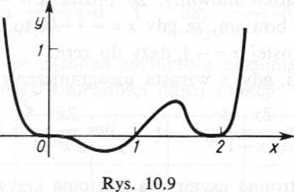
ł* . ^^atego, że / (x) jest wielomianem stopnia parzystego (szóstego) i współczynnik przy ^ dodatni (patrz zad. 5.11).

^{y r}«s funkcji y — x³(x— 1) (x — 2)² podany jest na rysunku 10.9.

i

Waliza

Matematyczna cz. I