043 5

Badanie przebiegu zmienności funkcji

2. Punkty wspólne z osiami OX, OY. oś OX

Badanie przebiegu zmienności funkcji

f(x) = 0, x -t--= 0    / ■ x, x 0

Szukamy miejsc zerowych funkcji. Otrzymane równanie jest sprzeczne, nie ma rozwiązań w zbiorze liczb rzeczywistych.

X² + 1 = 0

x~ = -1 równanie sprzeczne

Funkcja nie ma punktów wspólnych z osią OX.

oś OY

X0) nie ma sensu, ponieważ zero nie należy do dziedziny funkcji. Nie ma punktów wspólnych z osią OY.

3. Parzystość i nieparzystość funkcji

f(x) = * + —

/(-*) =

X

=>/(-*) = -/(*)

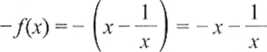
Funkcja jest nieparzysta.

Jeżeli funkcja jest nieparzysta, to jej wykres jest symetryczny względem początku układu współrzędnych (0; 0).

4. Granice

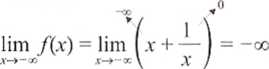
Korzystamy z faktu, że granicą sumy dwóch funkcji jest suma granic tych funkcji (stąd wyniki).

i —oo

Brak asymptoty poziomej

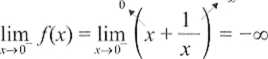
+00

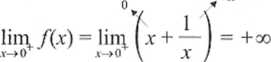
Asymptota pionowa istnieje i ma równanie x= 0.

Asymptota ukośna

y- ax + b, gdzie a = lim

l) = lim ( f{x) - ax)

X    *->**>

a = lim

.v->±co

/(-V)

*

1

X+ —

= lim-—

x—> ± cc X

= lim (--

.V—> ±y x

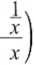
1₁

= lim

.V—> - cc

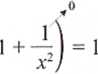
czyli

a =

b - lim (J[x) - ax) = lim (x + — - 1 x) = lim (/ +--/] =

,v->±oo    x->±& \ X    / .v->±ocy X )

Istnieje asymptota ukośna i ma równanie y - x

Korzystamy ze wzoru na pochodną ilorazu dwóch funkcji

= lim —= O, czyli b = O

.t-C=jc X

5. Pochodna

(1)'•*-(*)'• 1 .0-1 1 “¹⁺    7

6-7. Monotoniczność i ekstrema funkcji

/'(*)=! ¹ ^

W.K

/'W = Oo-y = 0 a:² - 1 = O

a: = 1 lub x = -1

85