035 4

Badanie przebiegu zmienności funkcji

Twierdzenie: Asymptota ukośna

Prosta y = ca + b jest asymptotą ukośną wykresu funkcji y = /(x), wtedy gdy: f(x)

a = lim -—- i b = lim [ f(x) - ax]

.V—>±'VD X    .V—> ±CC

BADANIE PRZEBIEGU ZMIENNOŚCI FUNKCJI - przykładowe zadania ZADANIE 1

Zbadaj przebieg zmienności funkcji i naszkicuj jej wykres:

f(x) = - ~x^A + x² + 1 Rozwiązanie

Jest tak dlatego, że funkcja fto wielomian określony w zbiorze liczb rzeczywistych. Przedział +x) to inny zapis zbioru liczb rzeczywistych.

Aby znaleźć punkty wspólne z osią 0X, należy wzór funkcji przyrównać do zera. W tym przypadku rozwiązujemy równanie dwukwadratowe, podstawiając pomocniczą niewiadomą.

+ 8= 12

Uzyskane wartości t_x, t_t wstawiamy ponownie do równania t - f. Wartość f, = 1 - v^l3 należy wyeliminować, ponieważ jest mniejsza od zera.

1.    Dziedzina funkcji

D= R = (-oo, +co)

2.    Punkty wspólne z osiami OX, OY oś OX

— —.V⁴ + x² + 1 = 0 /•(—2)

2

X⁴ - 2x² - 2 = 0 x² = /, f > 0 f - 2r - 2 = o

A = Ir - 4ac = (-2)² - 4 • 1 • (-2) = < = v'i 2 = -JTT = x<4 ■ V3 = 2 • t/3

2-2x13 2	2	2x5
	2 "	2
{ 2 + 2x5	2	2x5
	2 '	2
Zatem

X² = 1 + V3

x = VI + V3 lub x=-Vl + V3 Czyli

A = (—Vl + V3,0); B = (Vl + V3 , 0)

Badanie przebiegu zmienności funkcji

1    Aby odnaleźć punkty wspólne z osią 0X należy

./(0) ^{= —} T ‘ 0 + 0“ + 1 — 1    obliczyć wartość funkcji w punkcie x = 0.

oś OY

czyli

C = (0, 1)

3. Parzystość i nieparzystość funkcji

Funkcja y = /(x) jest parzysta <=>    [(-x) e D_f=s> f(x) =f(~x)\

Funkcja y =/(x) jest nieparzysta <=>    [(-x) e D_f =>/(-.v) = —/(x)]

Zatem sprawdzimy, czy nasza funkcja jest parzysta (wykres funkcji parzystej jest symetryczny wzglądem osi OY)

f(x) = -^[2x' + x- + 1 /(-*) = -“ (-x)¹ + (-x)² +

— X¹ + X² + 1 2

=>/(*) =/(-x)

funkcja jest parzysta

licząc granicę w -co wyłączamy x w największej potędze przed nawias, w nawiasie pozostaną funkcje, których granicę łatwo policzyć.

„ ( 1 X^2
= hm x^1 I---1—t	H—7
v ^2 -f^4	X^1
/ 1 1
= lim x^1 I---b —- \ 2 x^2

Czyli

lim f(x) = - co

X—>-cc

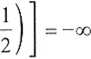
lim f(x) = lim (- ;-x¹ + x² + 1

.V—> + oc    .V—> —KO \ 2

Licząc granicę w +=o postępujemy tak jak poprzednio.

= lim x¹

X—►—+CC

69

1

Granice

lim /(x) = lim (—x¹ + x² + 1

x~^>~”    x^->““\ ²