111

X. Badanie przebiegu zmienności funkcji

375-

imetru) błąd procentowy pomiaru jest proporcjonalny do wielkości tg x+ctg x,

jest kątem wychylenia wskazówki galwanometru. Przy jakim wychyleniu x błąd

jdzie

W przedziale 0<a<iit pochodna dVjda przybiera wartość 0, gdy lga=\yfl, czyli a=35°16'.

Gdy kąt a zmienia się od wartości a<35°16' do wartości a>35°16', pochodna dVji-zmienia znak z dodatniego na ujemny (ponieważ w pierwszej ćwiartce cosinus maleje a sinus rośnie), a więc objętość V osiąga maksimum.

A więc stożek wpisany w kulę ma największą objętość, gdy kąt rozwarcia jest 70°32’ Łatwo obliczyć, że jeżeli tga=£,/2, to cos a = Vf i sin a=VJ, a wówczas r= jRy/2, h=±R.

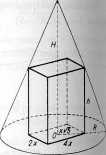
Zadanie 10.46. W stożek obrotowy o promieniu podstawy R i wysokości AT jest wpisany prostopadłościan. Stosunek boków podstawy prostopadłościanu wynosi 2. Obliczyć wy. miary prostopadłościanu o maksymalnej objętości.

Rozwiązanie. Oznaczmy boki podstawy prostopadłościanu odpowiednio przez 2x i 4x, a wysokość przez h (rys. 10.38). Przekątna podstawy prostopadłościanu wynosi 2xj5. Wysokość prostopadłościanu wyznaczmy z proporcji:

h R-xj5    „K-*s/5

—=-— , skąd h=H —-— •

HR    R

Objętość prostopadłościanu wynosi V=2x-4x h, czyli

,R-xj5 K = 8Hx²    ■

dV    24Hx*j5

Obliczmy pochodną —=16Hx----, czyli

dx    R

dx R

Pochodna dV/dx jest równa zeru, gdy x=0 albo gdy x=

Obliczmy drugą pochodną

d²V 1677    -

<^R-³*V3.

Gdy x=-^L mamy    < 0, więc funkcja V osiąga maksimum.

3,y 5    dx

-y tej wartości x promień koła opisanego na podstawie prostopadłościanu wynosi i$--R> ^a wysokość prostopadłościanu jest h=\H.

Jadanie 10.47. Przy pomiarze natężenia prądu za pomocą busoli stycznych (rodzaj

kiwano”

Procentowy będzie najmniejszy?

Rozwiązanie. Obliczmy pochodną

<i(tgx+ctgx) sin² x—cos² x    4cos2x

dx    cos² x sin² x    sin²2x

Przyrównując pochodną do zera i badając drugą pochodną, otrzymujemy x_min = 45°

Zadanie 10.48. Pole S przekroju pewnej części przewodzącej prąd / o natężeniu 5 ampe-_r5w zmienia się według wzoru

_c 2x² + l    ₂

S=—=- mm ,

x² + l

gdzie x jest współrzędną punktu, w którym badany jest przekrój S. Obliczyć, ile wynosi maksymalna gęstość natężenia prądu, która wyraża się wzorem j—i/S.

Rozwiązanie. Wyznaczamy gęstość natężenia prądu dla dowolnego punktu x przewodnika:

,₌_i₌_5__x²+l

^J S 2x² + l ⁵ 2x² +1 x² + l

Obliczamy pochodną

dj __<!2x(2x² + 1)-4x(x² + 1)    2x

dx    (2x² + l)²    (2x² + 1)²'

^ochodna djjdx równa się zeru, gdy x=0. Gdy x przechodzi od wartości x<0 do wartości • pochodna djjdx zmienia znak z dodatniego na ujemny, a więc w punkcie x=0 funkcja maksimum, które wynosi 5 A/mm².

lnduJ^^DA1^^IE -10.49- Natężenie prądu 7 w obwodzie zawierającym oporność czynną R, ^cyjność L i pojemność C połączone w szereg wyraża się wzorem

R² +((oL--)

^Wart°śei ^naP‘^^c‘^em P^r4du zmiennego przyłożonego do obwodu. Obliczyć, dla jakiej pulsacji co natężenie prądu I w danym obwodzie osiąga maksimum.