102 2

202 X. Badanie przebiegu zmienności funkcji

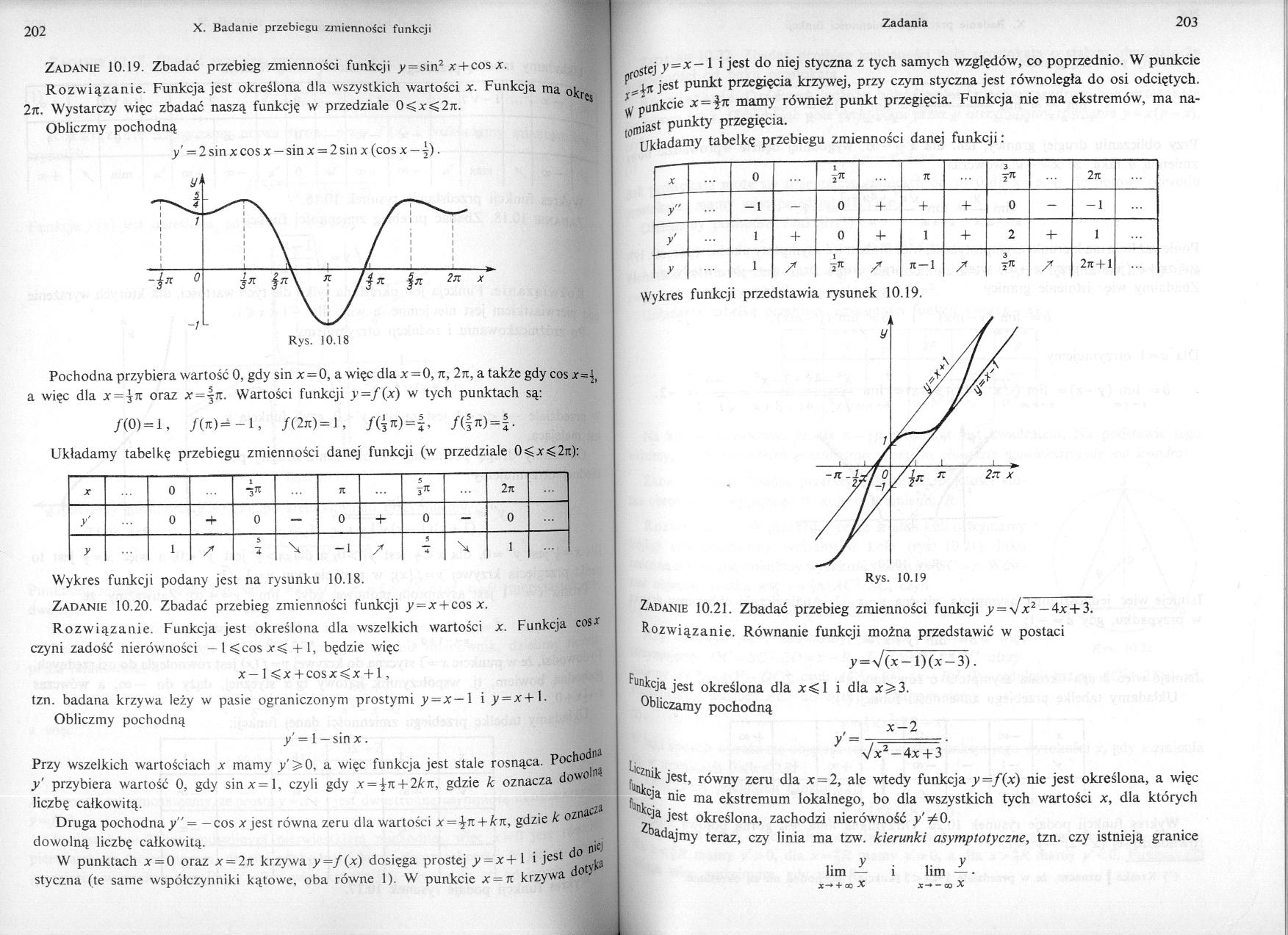
Zadanie 10.19. Zbadać przebieg zmienności funkcji _y = sin² x + cos x. Rozwiązanie. Funkcja jest określona dla wszystkich wartości x. Funkcja ma ok 2tc. Wystarczy więc zbadać naszą funkcję w przedziale 0<x<2;t.

Obliczmy pochodną

y' — 2 sin x cos x - sin x = 2 sin x (cos x - i).

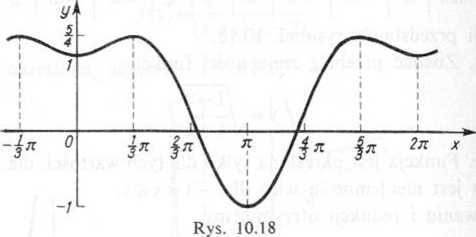
Pochodna przybiera wartość 0, gdy sin x = 0, a więc dla x = 0, n, 2ji, a także gdy cos x=j, a więc dla x = ^7t oraz x=|rr. Wartości funkcji >’=/(x) w tych punktach są:

/(0) = 1, /(it)— — 1,    /(2n) = 1,    /($ 7t)=|,    /(|tt)=|.

Układamy tabelkę przebiegu zmienności danej funkcji (w przedziale 0^x<2it):

X		0		1 ~^n		K		5 3*		2tt
/		0	+	0	—	0	+	0	-	0
y		i	/	5 4	\	-i	/	5 T	\	1

Wykres funkcji podany jest na rysunku 10.18.

Zadanie 10.20. Zbadać przebieg zmienności funkcji y = x + cosx.

Rozwiązanie. Funkcja jest określona dla wszelkich wartości x. Funkcja cos* czyni zadość nierówności — 1<cosx<+1, będzie więc

x— 1 <x+cosx<x + l,

tzn. badana krzywa leży w pasie ograniczonym prostymi y = x-1 i y = x+l-Obliczmy pochodną

y' = 1 — sin x.

Przy wszelkich wartościach x mamy y'^0, a więc funkcja jest stale rosnąca. Pochody y' przybiera wartość 0, gdy sinx=l, czyli gdy x = j-n+ 2kir. gdzie k oznacza do'^° liczbę całkowitą.

nid

jca

do

Druga pochodna y"= —cos xjest równa zeru dla wartości x = ^K + kir, gdzie k ol dowolną liczbę całkowitą.

W punktach x = 0 oraz x = 2k krzywa y=f(x) dosięga prostej y = x+l i j^est

styczna (te same współczynniki kątowe, oba równe 1). W punkcie x=n krzywa doO

x- 1 i jest do niej styczna z tych samych względów, co poprzednio. W punkcie punkt przegięcia krzywej, przy czym styczna jest równoległa do osi odciętych. _unJSVIv! x=$n mamy również punkt przegięcia. Funkcja nie ma ekstremów, ma na-15ast punkty przegięcia.

prostej y-

*j^est

Układamy tabelkę przebiegu zmienności danej funkcji:

X		0		1 2^K		n		3 2*		2n
y"		-i	-	0	+	+	+	0	-	-i
y'		i	+	0	+	i	+	2	+	i
y		i		l^n	/	TC —1		3 3*	/	2n + l

Wykres funkcji przedstawia rysunek 10.19.

Zadanie 10.21. Zbadać przebieg zmienności funkcji y = \Ix²-Ax+2>. Rozwiązanie. Równanie funkcji można przedstawić w postaci

y = V(x-l)(x-3).

fikcja jest określona dla x^l i dla x^3.

Obliczamy pochodną

x—2

/ =

yjx²-4x + 3

^Llctnik

. 7 Jest, równy zeru dla x = 2, ale wtedy funkcja y=/(x) nie jest określona, a więc fonlc^ ⁿ*^{G ma ekstremum} lokalnego, bo dla wszystkich tych wartości x, dla których jest określona, zachodzi nierówność y' / 0. udajmy teraz, czy linia ma tzw. kierunki asymptotyczne, tzn. czy istnieją granice

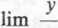
1

lim Z.

x~* + oc X - oo X