137 2

272 XI[t. Badanie przebiegu zmienności funkcji

Zadanie 13.4. Zbadać przebieg zmienności funkcji y= — .

In x

Rozwiązanie. Funkcja jest określona dla x>0 i x#l. Obliczmy pochodną

^ ln x ( ln a:)

Pochodna równa się zeru, gdy lnx=l, czyli gdy x = e; wtedy f(e) = e. Obliczmy drugą pochodną

y

tt

2 —lnx x(Inx)³

Druga pochodna równa się zeru, gdy lnx=2, czyli gdy x = e²; wtedy /(e²) = ^_e2 Obliczmy granice

lim y = 0

x- + 0

(gdyż licznik dąży do zera, a mianownik do - oo) oraz

lim / = lim (-

x-» + o x— + o\lnx

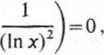
a więc krzywa przy x-» +0 zbliża się stycznie do osi Ox. Gdy x-+l +0, to In x-++0, czyli y-* + oo, gdy zaś x-»l -0, to ln x-*-0, czyli y-+ — oo, a więc prosta x=l jest asymptotą pionową krzywej w obu swoich zwrotach.

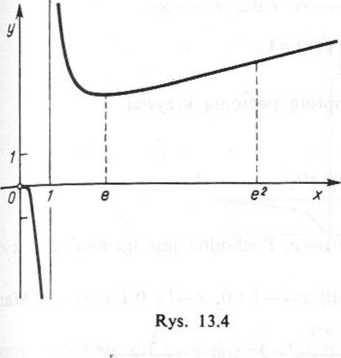
Krzywa ma minimum w punkcie x = e i punkt przegięcia, gdy x = e².

Układamy tabelkę przebiegu zmienności danej funkcji:

X	0		1			e		e^2	...	— CO
y"	— 00	-	— 30	+ oo	+	+	+	0	-	0
y'	0	—	— CO	— 00	-	0	-+•	—	4-	0
y	0		— co	— 00	\	e	/•	1	/	+ eo

Wykres funkcji podaje rysunek 13.4.

Zadanie 13.5. Zbadać przebieg zmienności funkcji y = (x² — 3) e^x.

Rozwiązanie. Funkcja jest określona dla wszystkich x.

Obliczmy pochodną

/ = (x²+2x —3)e^x.

Pochodna równa się zeru, gdy x=—3 i gdy x=l; wtedy /(-3) = 6e“³, /0)⁼"qr '

Obliczamy drugą pochodną

y"=(x²+4x-l)e^x.

Miejscami zerowymi drugiej pochodnej są liczby a= —2 — y/Ś i 0=-2 + ^/5.

Obliczmy granicę

lim (x²- 3)e^x= + oo.

x~* + oo

Natomiast aby obliczyć lim f(x), podstawiamy x=—u; wówczas otrzymujemy (patrz

X~* — oo

wzór (12.2.5)):

2_3

lim f(x)= lim (u²-3)e^_"= lim ■~=0.

JC-*-00    U-* + CO    u-* + CO £

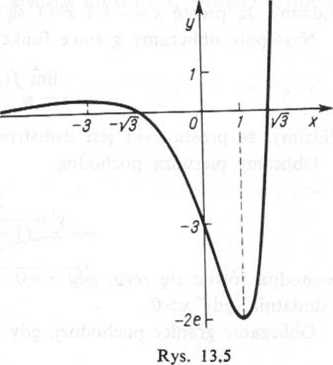
Krzywa ma jednostronną asymptotę poziomą y = 0, maksimum w punkcie x= — 3, minimum w punkcie a: = 1, punkty przegięcia, gdy x= —2 — ^/5 i gdy x—— 2 + _v/5. Układamy tabelkę przebiegu zmienności danej funkcji:

X	— 00		ct		-3		P		1
y"	0	+	0	-	-	-	0	+	+	+	4-oo
y'	0	4-	■+	+	0	—	-	-	0	+	+ oo
y	0	/	/(*)		6e-^3	\	/(/?)	\	—2e	/	+ oo

Wykres funkcji podaje rysunek 13.5.