044

Badanie przebiegu zmienności funkcji

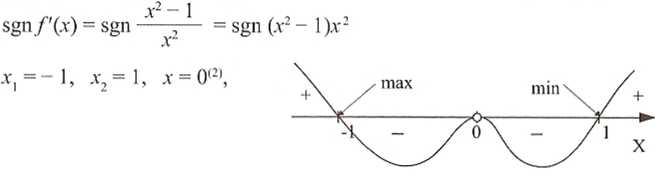
x e (-co; -1) =>/(.x) 7¹ je(-];0) =>/(*) \ x e (0; 1) =>/(x) \

.v e (1; +oc) =>/(*) 71

8. Tabelka

X G		-1	(—1; 0)	0	(0; 1)	1	(1»^+°°)
m	+	0	-	X	-	0	+
m		max		X		min

9. Wykres

ZADANIE 6

Zbadaj przebieg zmienności i naszkicuj wykres funkcji: f(x) = -x⁴ + 2x²

= lim

.v—> ~ o

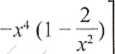
= [-00 • 1] = -00

r

Badanie przebiegu zmienności funkcji

Rozwiązanie:

1.    Dziedzina funkcji

D= (-00, +oo)

2.    Punkty wspólne z osiami OX, OY. oś OX

/(x) = ()<=> —X'¹ + 2x² = O

-x² (x² - 2) = O

-x² (x + V2)(x -V2) = 0

x = O lub x = -t/2 lub x = ^2

A = (O, 0),B = (-V2, 0),C = (V2, 0),

oś OY

/(O) = - (O)⁴ + 2 • (O)² = O D = (O, 0)

Dziedziną jest zbiór liczb rzeczywistych, ponieważ badaną funkcją jest wielomian.

Rozwiązujemy równanie wielomianowe, wyłączając -X przed nawias i rozkładając - 2 na czynniki liniowe.

wzór y - / = (x + y)[x - y)

3. Parzystość i nieparzystość funkcji

/(x) = -X⁴ + 2x²

/(-x) = -x⁴ + 2x²

-/W = - (-X⁴ + 2x²) = x⁴ - 2x²

Wynika stąd, że funkcja jest parzysta.

4. Granice funkcji

=>/W=/(--v)

Asymptoty pionowej nie ma, gdyż dziedziną funkcji jest zbiór R.

lim /(x) = lim (-X⁴ + 2x²) =

.V—»-J£    ,V-»-TC

Licząc granicę wielomianu, wyłączamy xw najwyższej potędze przed nawias. W nawiasie znajdują się funkcje, których granicę policzyć bardzo łatwo.

lim /(x) = lim (-X⁴ + 2x²) =

= lim

Af—>4-30

= [-CC • 1] =-G0

Asymptota pozioma nie istnieje.

0*“

87