103 2

204    X. Badanie przebiegu zmienności funkcji

Obliczmy pierwszą granicę

lim — = lim —-— = lim

Przy obliczaniu drugiej granicy, tzn. dla x-» -co, wygodniej będzie wprowadzić

nową

u    Vu²+4u + 3

lim —= lim -——--^{— 1} ■

Ponieważ linia ma kierunki asymptotyczne, więc może mieć asymptoty ukośne: (por. str. 197) y=ax+b (jedną przy x-*co, wtedy a= 1, oraz drugą przy x->-oo, wtedy a=-j)    ¹

Zbadajmy więc istnienie granicy

b= lim (y—mx) i 6= lim (y—mx).

4x +3 —x²    -4

-4x + 3+x >/T +1

(') Kreska | oznacza, że w przedziale l<x<3 funkcja i pochodni

y=-x +px.

Rys. 10.21

y'=|jtx(4/l—3x).

la x-

zmTenną « taką, że x=-«; wówczas

Dla a= 1 otrzymujemy

b= lim (y-x) = lim (Vx²-4x+3-x)= In

Istnieje więc jednostronna asymptola ukośna y = x — 2. Analogicznie obliczamy granice w przypadku, gdy a = - 1:

b= lim (y+x)=2.

Istnieje więc druga ukośna asymptota o równaniu y=—x + 2.

Układamy tabelkę przebiegu zmienności funkcji ('):

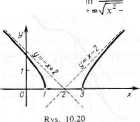
Wykres funkcji podaje rysunek 10.20. Otrzymana lima jest górną połową równoosiowej (x - 2)^ł - y² = 1.

ą olrreślone.

2ADANIE 10.22. Zbadać przebieg zmienności pola prostokąta o stałym obwodzie 2p . zależności od boku prostokąta.

Rozwiązanie. Oznaczmy jeden z boków przez x; wówczas drugi bok prostokąta jjt równy p—x. Oznaczając póle prostokąta przez y otrzymujemy równanie y=x(p—x),

(0

Bok prostokąta może się zmieniać w granicach od x=0 do x=p, tj. do połowy obwodu prostokąta; mamy więc przedział OsSxsSp.

Obliczamy pochodną funkcji (1):

y'=-2x+p.

I pochodna równa się zeru dla x=\p i jest dodatnia dla x<\p, a ujemna dla x>\p. Dla I _x=lp otrzymujemy maksimum pola równe \p².

Układamy tabelkę przebiegu zmienności funkcji y=x(p-x):

X	0		ip		p
/	+	+	0	-
y	0	/	xP^2	\	^0

Na koniec zauważmy, że dla x-^p prostokąt jest kwadratem. Na podstawie tego widzimy, że ze wszystkich prostokątów o stałym obwodzie największe połę ma kwadrat.

Zadanie 10.23. Zbadać przebieg zmienności objętości stoika obrotowego wpisanego w kulę o promieniu R.

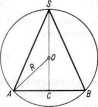
Rozwiązanie. W przekroju przez środek kuli otrzymamy trójkąt równoramienny wpisany w koło (rys. 10.21). Jako zmienną niezależną obierzmy wysokość stożka/i = SC=x. Wów-^czas objętość stożka jest y=%n-AC² ■ SC, czyli ⁽¹>    y = ±nx-AC².

Aby obliczyć AC², zauważmy, że AO = OS=R, a więc I ^otrzymujemy OC=SC-SO = x-R. Z trójkąta AOC otrzyjmy AC²=A0²-0C², czyli AC² = R²—(x— R)². Po redukcji mamy AC²=2Rx—x². tawiąjąc wartość AC² do wzoru (1) otrzymujemy y-±xx*(2R-x).

sit^* ^sP°^sób wyraża się objętość stożka y jako funkcja jego wysokości x, gdy x zmienia granicach 0<x<2R.

Wliczamy pochodną funkcji (2):

ponieważ x^0, więc znak pochodnej jest taki sam, jak znak wyrażenia 4R — 3x, tzn. osj mamy y'>0, dla x=fi? mamy y'=0, a dla x>|J? mamy /<0. Funkcja (2) "'ięc maksimum, gdy x=^R.