105 2

208 X. Badanie przebiegu zmienności funkcji

Obliczamy pochodną

dx V x³ (d — x)³J

Przyrównując pochodną do zera otrzymujemy x = d/( 1 + \J2). Pochodna jest ujemna 0<x<d/(\ +\J2) albo gdy x>d, a dodatnia, gdy *<0 albo gdy <//(! + \j2)<x<d. z_ate^

(1 +l/2)³ke

ke

^,IW4?-

Układamy tabelkę przebiegu zmienności funkcji K(x):

X	— GO		0			d 1+^2		d			+ 00
dK(dx	0	4.	+ oo	— 00	—	0	+	-f 00	— 00	-	0
K(x)	0	/	+ oo	4-co	\	•^min	/	+ 00	+ 00	\	0

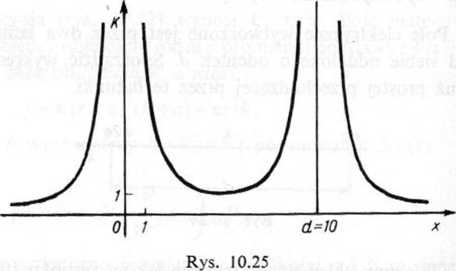
Sporządzamy wykres funkcji K(x) przyjmując ke~ 10,    = 10 (rys. 10.25).

Zadanie 10.27. Pole elektryczne wytworzone jest przez dwa ładunki punktowe +^e i +2e, które są wzajemnie oddalone o odcinek d. Sporządzić wykres natężenia K p°'^a elektrycznego wzdłuż prostej przechodzącej przez dane ładunki.

Rozwiązanie. Obierzmy układ współrzędnych jak na rysunku 10.26.

+e

T

X

-

+2e

T7

d

Rys. 10.26

Zgodnie z prawem Coulomba natężenie K wyraża się wzorem

k jest to współczynnik zależny od wyboru jednostek. Funkcja ta jest określona wszystkich wartościach x z wyjątkiem 0 i d. Granice funkcji w punktach nieciągłości

przy ^noszą:

lim K(x)= +<X), lim K(x)=+ co, lim K(x)~ - co, lim K(x)= - co,

x-* + 0

x~*d — 0

x->d-0

więc proste x = 0 i x=d są asymptotami pionowymi. Ponadto zauważmy, że

lim K(x)= lim K(x) = 0,

x~* - 00    x~* + 00

więc prosta K=0 jest asymptotą poziomą. Obliczamy pochodną

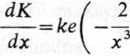
O*-*)³}

Przyrównując pochodną do zera otrzymujemy x=dj(\ — \j2). Układamy tabelkę przebiegu zmienności funkcji K(x):

Rys. 10.27

X	— 00		d i-V5		0			d			+ co
dK/dx	0	-	0	+	-f-oc	— 00	-		+ 00	+	0
K(x)	0	\	■^min	/	-r oo	-ł- CO	\	— 00	— co	/	0

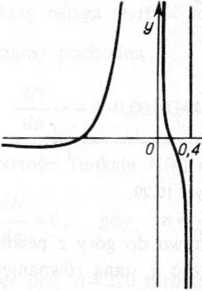
Sporządzamy wykres funkcji K(x) przyjmując ke= 1, d-0,4 (rys. 10.27).

lft ^^ADANIE 10-28. Natężenie prądu i płynącego w obwodzie przedstawionym na rysunku ■28 jest określone wzorem

(1)

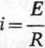
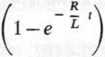
Udzie £

oznacza siłę elektromotoryczną źródła prądu stałego, R — oporność obwodu,