107 2

212 X. Badanie przebiegu zmienności funkcji

Rozwiązanie. Obliczamy pochodną

— = 2 • 0,0000105884f - 0,000599201. dt

Obliczamy, przy jakich wartościach t funkcja c(t) osiąga ekstremum:

— = 0, gdy dt

59,9201

2,11768

28,3°

Ponieważ d²cfdt²>0, więc przy temperaturze r = 28,3° funkcja c(f) osiąga minimum które wynosi c = 0,99813.

Zadanie 10.33. Statek płynący na południe z prędkością 10 węzłów przecina w punkcie A kurs drugiego statku, który płynie na wschód z prędkością 15 węzłów (¹). Gdy pierwszy statek był w punkcie A, drugi znajdował się w odległości 30 mil morskich przed tym punktem. W którym momencie odległość między statkami jest najmniejsza?

Rozwiązanie. Zaczynamy obliczanie czasu w chwili, gdy pierwszy statek znalazł się w punkcie A. Droga przebyta przez pierwszy statek wynosi y— lOr, a droga drugiego statku y=15(f-2). Kwadrat odległości między statkami wynosi

s² = 15²(z—2)² +10²/².

Różniczkując obie strony tej równości względem czasu:

ds

2 s—= 450(r-2)+200f dt

i przyrównując pochodną do zera otrzymujemy t*l godz 23 min.

Zadanie 10.34. Pewna siła działająca wzdłuż drogi x wykonuje pracę określoną wzorem L=l— e~^2x2. Wyznaczyć, w którym miejscu drogi (jc>0) wartość siły F=dL\dx osiąga maksimum.

Rozwiązanie. Obliczamy

— 2x²

F =

dL

— = 4xe dx

Aby znaleźć maksimum tej funkcji, obliczamy jej pochodną dF

— = 4e ” ^2x2 -16x²e ' ^2x2 = 4 (1 - 4x²) e ~ ^2x\ dx

Przy dodatnich wartościach x pochodna przechodzi przez 0 w punkcie x = |, przy zmienia znak z dodatniego na ujemny. A więc w punkcie x = ^ siła F osiąga maksim^uin’ które wynosi F=2e~* = 0,765.

(‘) Mila morska jest to długość jednej minuty południka ziemskiego i wynosi 1852 m. łkfze/j** jednostka prędkości równa jednej mili morskiej na godzinę, czyli 1,852 km/h.

Zadanie 10.35. Siła F, skierowana pod kątem 9 do poziomu (rys. 10.30), potrzebna poruszenia z miejsca ciała o ciężarze G wynosi

F= -

fiG

cos#+/rsin 9

H_Zie fi j^est współczynnikiem tarcia. Obliczyć kąt 9, przy którym siła F potrzebna do przesunięcia ciała jest najmniejsza.

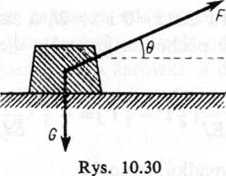
Rozwiązanie. Wartość Fjest najmniejsza przy takiej wartości kąta 9, przy której funkcja /(0)=cos 9+fi sin 9 jest największa.

Obliczamy pochodną mianownika

/'(#) = — sin(ł+^cos0.

Pochodna ta przybiera wartość 0, gdy tg 9=fi, czyli 0 = arc tg fi.

Obliczamy drugą pochodną

/"($)= — cos0—fi sin 9.

Przy 0=arc tg fi mamy f"(6)<0, więc funkcja/(6) osiąga maksimum, a siła F minimum.

Kąt 9₀, spełniający równanie tg9₀-fi, nazywamy kątem tarcia. Gdy siła działająca na ciało jest nachylona do poziomu pod kątem 6₀, wówczas mamy

p    /iG    G tg 9 ₀

cos9₀+fisind₀ cos0_o+tg0_osin0_o ^co Po przekształceniu daje F— G sin 8₀.

Rys. 10.31

. ^^a°anie 10.36. Ugięcie y belki zamocowanej z jednej strony (rys. 10.31), wyrażone ^Ce>itymetrach, oblicza się według wzoru

P

Tj'

k=^(|x³-i/x²),