99 (74)

196

Rozwiązanie

Oznaczmy momenty okręcające w utwierdzeniach M. i Mg. Równanie równowagi względem osi ma postać

Z"o    ^ - °-

W równaniu powyższym występuję dwie niewiadome, mamy zatem zadanie statycznie Jednokrotnie nlewyznaczalne.

Drugie równanie otrzymamy rozpatrując odkształcenia. Kąt skręcenia końcowych przekrojów wału A i 0 względem siebie jest równy zeru, bo przekroje są utwierdzone. Aby rozwiązać zadanie wystarczy sformułować równania określające wspomniany kąt skręcenia w funkcji momentów obciążających wał. Kąt ten Jest sumą algebraiczną kątów skręcenia poszczególnych odcinków wału, wzdłuż których zarówno moment skręcający wał, jak i średnica wału są stałe. Przyjmuje się przy tyn umowę odnośnie znaku kąta skręcenia. Patrząc na wał od prawego końca, za dodatni uważa się taki kąt, który skręca wał w śrubę prawoskrętną 1 odwrotnie, za ujemny uważa się teki kąt, który skręca wał w śrubę lewoskrętną. Umowa ta jest konsekwencją przyjętych znaków momentów w równaniu równowagi. Łatwo można zauważyć, że w lewej połowie wału moment skręcający równy Jest momentowi M,,a w prawej momentowi Mg.

Ostatecznie równanie określające kąt skręcenia końcowych przekrojów wału A i O względem siebie przyjmuje następującą postać:

Po uproszczeniu otrzymuje się równanie

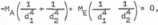
z którego wynika, że

^ma ^{= m}e'

Podstawiając powyższe do równania równowagi otrzymujemy

-Mg ♦ M_c - Mg

Takę sarnę wartość na równia! moment M.. Wynik ten był do przewidzenia bez przeprowadzenia obliczeń, gdy! układ Jest symetryczny względem płaszczyzny, w której działa moment M_c. Wykres momentów skręca-Jęcych M przedstawia rys. I1.50b.

Wartości maksymalnych naprężeń tnęcych oblicza się ze znanego wzoru, przy czym odpowiednie wskaźniki wytrzymałości przekroju wy-

#(4.0 • 10^-2)³

16- ^-

#(6,0 • 10^-2)³ -¹ IB-    "

1,26 • 10^-5 4,24 • 10^-5

r. > -—- . 39,68 MPa,

^AB 1,26 • 10“⁵

r ■-—    .6 • 11.79 MPa,

^BC 4,24 • 10 ^S

11,79 MPa.

6t«d

Mg * 0,5

500 Nm.

CD ‘BC

- 39.68

Znak ujemny w przypadku naprężeń ^rC0 ^{1 r}0E pominięto, gdy dla przypadku skręcania obojętny jaat znak naprężenia, a decyduje Jego wartość liczbowa.

II.3.11. Stalowy wał AD (rys. n.5la) utwierdzony obu końcami, wydrężony wzdłuż całej swej długości, o średnicach d^ ■ 50 mm, d_g . • 40 mm, dj ■ 30 aa, jest obciężony momentami akręcajęcyml M >

■ 1 kNm, M ■ 0,2 kNm. Obliczyć maksymalne naprężenia styczne we wszystkich przedziałach wału.

Odpowiedź. Wykres momentów skręcajęcych M przedstawia rys. II.51b. Maksymalne naprężenia tnęce wynoszę:    ■ 31,83 MPa,

f_QC ■ 14,98 MPa,    • 13,97 MPa.