295 (18)

294 Rozdział 5. Układy regulacji impulsowej

Rozwiązanie

Oznaczmy:

K (s) = K„ (s) K, (s) lub K (s) = Ki (s) K, (s) K_x (s).

W przypadkach a), c) i d) część ciągła układu ma transmitancję K (s).

Oznaczając odpowiadającą jej transmitancję dyskretną przez K (z), otrzymujemy równanie charakterystyczne układu zamkniętego

m (z) [1 + K (z)] = 0.    (1)

Zatem warunki stabilności dla układów a), c) i d) są identyczne.

W przypadku b) część ciągła układu jest rozdzielona impulsatorem, a więc zarówno na K₀(s), jak i na K„ (s) wchodzą impulsy z impulsatora. A zatem równanie charakterystyczne układu zamkniętego ma w tym przypadku postać:

m₀ (z) m_a (z) [1 -I- K₀ (z) K, (z)] = 0,    (2)

gdzie: K₀ (z) i K_s (z) są transmitancjami „z” odpowiadającymi częściom ciągłym o trans-mitancjach K₀ (s) i K_a (s). Wobec powyższego warunki stabilności w przypadku b) są odmienne niż w pozostałych.

Dla przypadku a) transformata „z” sygnału wyjściowego ma postać:

(3)

(4)

W„ (z) K₀ (z)

^y(2)

dla przypadku b)

W₀(z)K₀(z)

1 + K₀(z)K_a(_Sy

Dla przypadków c) i d) przekształćmy schematy blokowe w sposób przedstawiony na rys. 5.49 i 5.50.

Na rys. 5.49 v oznacza odpowiedź układu o transmitancji K₀ (s) na sygnał w₀, a na rys. 5.50 - odpowiedź układu o transmitancji K_x (s) na sygnał w₀.

Oznaczmy przez V (z) i V\ (z) transformaty tych sygnałów. Zwróćmy uwagę, że wprawdzie V (s) = W₀ (s) K₀ (s) oraz Vj (s) = W₀ (s) Ki (s), to jednak V (z) ^ W₀ (z) K₀ (z) oraz Vi(z)^iW₀(z)K_l (z).

Transformaty sygnału y, mają zgodnie ze schematami blokowymi postać:

- w przypadku c:

Y(z) =

V{*)

1 + K{z)'

(5)

— w przypadku d:

(6)

\/1 Vi(z)K₂(z) ^U 1 + K (z) ’

Tak więc mimo identycznych części ciągłych w każdym z tych układów przebiegi sygnałów wyjściowych są różne.

C)

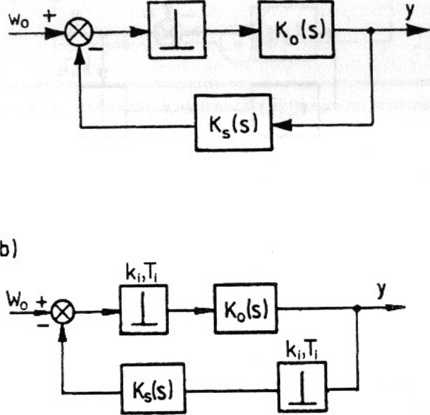
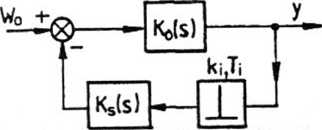
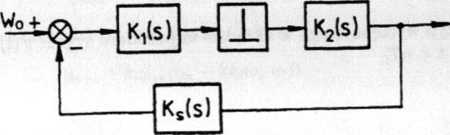
Rys. 5.48. Różne konfiguracje układów impulsowych