281 (19)

280 Rozdział 5. Układy regulacji impulsowej

otrzymujemy z³ + A„z² + A_tz + A₂ = 0.

W celu skorzystania z warunków Hurwitza podstawmy:

w + 1

* ~ w-r

czyli mamy

(w + l)³ + A„ (w + l)² (w - 1) + Ai (w - l)² (w + 1) + A₂ (w - l)³ = 0.

Zatem po uporządkowaniu:

w³ (1 + A₀ + Ai + ylj) + w² (3 + A₀ — Ai — 3A2) +

+w (3 — A₀ — Ai + 3^) + 1 ~ A₀ + Ai — A₂ = 0.    (15)

Skąd wynikają warunki stabilności

1 + A₀ + Ai + A₂ >0,

3 + A₀ - A\ - ZA₂ > 0,

3 - A₀ - Ai + 3A₂ > 0,

1 — A₀ + Ai — A2 > 0,

(3 + A₀ — Ai — 3A2) (3 — A₀ — Ai + 3A2) +

— (1 + A₀ + Ai + A2) (1 — A₀ + Ai — A2) > 0. (17)

Nierówność (17) można zapisać również w postaci:

(3 — A1)² — (A₀ — 3A2)² — (1 + A1)² + (A„ + A2)² > 0.    (18)

Warunki (16) i' (18) po podstawieniu A₀, Ai, A₂ są następujące:

kiT{ [&n + kiknk₂₂ — kiki₂k₂i (1 + A)] (1 — D) > 0,    (19)

(1 — D) [2^22 + 2 — k^kuk^Ti] + kikuTi (1 + D) +    /nrij

+k³ki₂k₂iTi^ [L - 3LD + 2D] > 0,    ^V

4 - kikuTi (1 -£>)(! + kik22) - k³k_uk₂iTi (4D - 3LD - L)    > 0,    (21)

— (1 — D) [2 + 2kikxi — kikiik^Ti] +

- kikuTi (1 + D)~ k³ki₂k₂iTj-j^ (L-2D + LD) > 0, (22)

3 - k*k_nk₂₂Ti (1 - D) - D + kik₂₂ (1 - D) + Dkik_nTi + ^k_nk_2iTi^-^ (L - D)

+

kikuTi — 1 — D 4- kik22 (1    D) — 3kf k\₂k₂\TiD (1 — L)

1 + A

+

,1 +A

1 + D + kfkuknTi (1 - D) - k_{k₂₂ (!-£>)- Dkik_uTi - k*k_l2k₂₁Ti-j— (L - D)

+

kikuTi — 1 + kik₂₂ (1 ^— IT) — D — kf k\₂k₂\TiD (1 — L)

14-A

> 0.    (23)

Uwaga: Przydatność otrzymanych nierówności do syntezy układu (doboru jego parametrów) jest bardzo mała, można z nich jednak korzystać przy analizie układu.

Zadanie 5.15

Na rys. 5.36 przedstawiono schemat blokowy układu impulsowego dwóch zmiennych. Porównać warunki stabilności układu w przypadku synfazowej i niesynfazowej pracy im-pulsatorów na płaszczyźnie (A:,i, k_l2)- Okres impulsowania w układzie jest tak dobrany, że obiekt można uważać za statyczny.

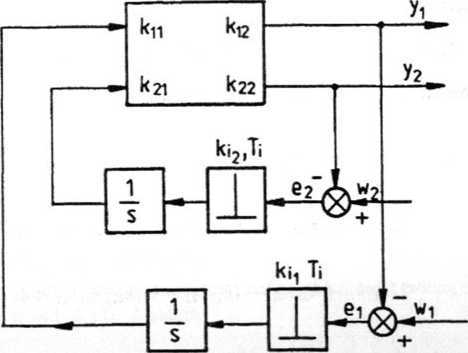
Rys. 5.36. Układ regulacji impulsowej dwóch zmiennych, ku > 0, k₂₂ > 0 Rozwiązanie

a) Impulsatory pracują synfazowo

część ciągła układu ma transmitancję macierzową:

- kn	k\2
s	s
k21	&22
- s	S

(1)

R(s) =