253 (19)

252 Rozdział 5. Układy regulacji impulsowej

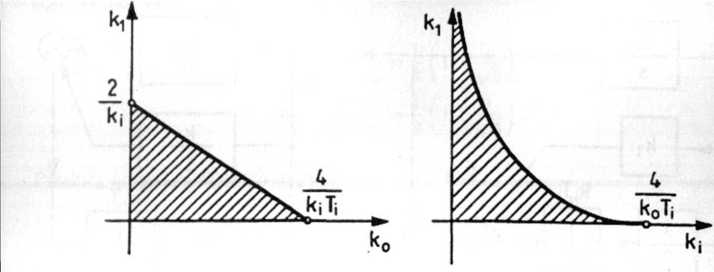
Rys. 5.12. Obszar parametrów zapewniających stabilność układu

Dla danych z zadania 5.2 nierówność (5) przyjmuje postać:

0 < k\ < 1,5.

Należy zwrócić uwagę, że jeśli

k,k₀T, > 4,

to układu nie da się ustabilizować w rozważany w zadaniu sposób.

Zadanie 5.4

Podać warunki stabilności dla przedstawionego na rysunku 5.13 układu regulacji impulsowej. Sprawdzić, czy układ jest stabilny dla k₀k, = 1. Jaki będzie uchyb w stanie ustalonym, w przypadku gdy tz;₀ = 1 (t) ?

Rys. 5.13. Schemat blokowy układu regulacji impulsowej z zad. 5.4 (0 < T₀ < Ti)

Rozwiązanie

Transmitancja operatorowa części ciągłej ma postać:

k eT⁹^⁰ = )•

K (z) = k₀ki

(L - D) z + D (1 - L) L(z-l)(z-D)

gdzie:

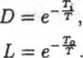
Równanie charakterystyczne układu zamkniętego ma postać:

Lz² + [k₀ki (L-D)-L-LD]z + LD + k₀k_xD (1 - L) = 0.

(3)

Po podstawieniu z = oraz uwzględnieniu, że:

A₀ = L, Ai = k₀ki (L — D) — L (1 + D), Ai — LD + k₀k{D (1 — Z#),

mamy zgodnie ze wzorem (5) z zad. 5.2 równanie:

k₀k,L (1 - D) w² + 2 [L (1 - D) - k₀kiD (1 - L)] w +

+2L (! + £>) + k₀ki [2D - L - LD) = 0.

(4)

Warunki stabilności można zapisać jako:

L (1 - D) - kgk_xD (1 - L) > 0; k₀k_x > 0, 2 L (1 +D) + k₀k_t (2 D-L- LD) > 0.

(5)

(6)

Warunek (5) da się przedstawić w postaci:

(7)

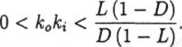
Warunek (6) jest spełniony, jeśli

2D - L - LD > 0,

(8)

lub jeśli

2D - L - LD < 0

(9)

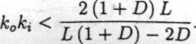
(10)