261 (19)

260 Rozdział 5. Układy regulacji impulsowej

uj — s/ićjći.

Stabilność układu badamy na podstawie równania charakterystycznego: z² + z(-2coswTi + kik sinuTi) + 1 - fc_iJfcsina/7' = 0.

(6)

Podstawiając:

z =

w + 1

w- r

otrzymuje się:

w²+ 2w + l +(w²- 1) (kik sin uTi - 2 cos ujT_{) + (w² - 2tu + l) (1 - sin wT)) = 0, w² (2 - 2cosuTi) + w (2kiksinuTi) + 2- 2k_tksin+ 2coswT; = 0.    (7)

Układ zamknięty jest więc stabilny, jeśli spełnione są nierówności:

1 > cos uTi,

kik sin u)Ti > 0,

1 - kik sin wT, + coswTi > 0.

Warunki (8) i (9) zachodzą, gdy:

ki > 0 oraz 21* < ujT_{ < (21 + 1) * gdzie: l = 0,1,2,...

czyli

21* < y/kjtlT, < (21 + 1) TT,

21*

(8)

(9)

(10)

^ rr _    (21 + 1) *

'    ~°’i’^2,"■

Warunek (10) jest spełniony, gdy:

1 > kiksinuTi - cosu/Tj = yjkfk² + 1 sin (u)Ti - (p),

(11)

gdzie

tg<p =

kik’

a więc, gdy

sin (uTi - ip) <

czyli

(12)

sin ( s/k₀k{Ti — arctg--=L

Układ będzie stabilny, jeśli spełnione są nierówności (11) i (12). Na przykład jeśli k₀ = ki = 1 [1] ,*» = !, to układ jest stabilny dla 0 < 7) < f.

Zadanie 5.9

Znaleźć transmitancję dyskretną układu z impulsatorem o skończonej szerokości impulsu 7 i obiektem o transmitancji

^K^ ⁼ r+sT ^^rys'^5-21)

Rozważyć przypadek, w którym szerokość impulsu jest równa zero oraz gdy jest równa okresowi impulsoowania T,. Zbadać stabilność układu po zamknięciu.

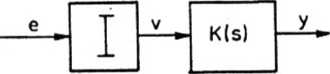
Rys. 5.21. Układ z impulsatorem o skończonej szerokości impulsu 7. Schemat blokowy układu

Rozwiązanie

Amplituda n-tego impulsu jest równa:

A_n = A;Je (n7J), a jego pole S„ = 7fcje (nTi).

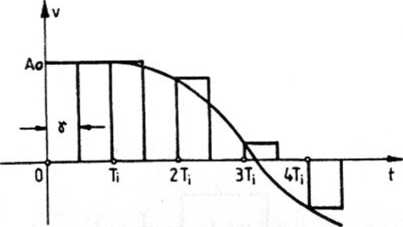
Rys. 5.22. Układ z impulsatorem o szerokości impulsu 7 Sygnał wyjściowy z impulsatora

Odpowiedź części ciągłej na pojedynczy impuls o amplitudzie k[ ma postać

k' (t) = [l - «-+] [1 (t) - 1 (t - 7)] + k\k₀ [l - e~*] e-^1 (t - 7) •    (1)

Wobec tego:

(2)

L

k' (nTi) ⁼ k\kJ^L—r^-Dⁿl (nTi—),