269 (19)

268 Rozdział 5. Układy regulacji impulsowej

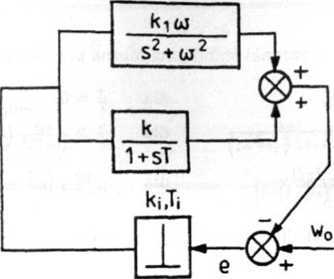
Rys. 5.27. Schemat blokowy układu regulacji impulsowej z zad. 5.11 Rozwiązanie

Transmitancję dyskretną układu otwartego można przedstawić jako:

K (z) = Ky (z) + K_i(z),    (1)

gdzie Ki (z) odpowiada części ciągłej o transmitancji:

(«) =

k

1 + sT’ a K2 (z) - części ciągłej o transmitancji

kiu)

s² + w²'

K2(S) =

Zgodnie ze wzorem (19) z zad. 5.1e) mamy:

K, (z) =

kik D ~T z-D'

Natomiast ze wzoru (4) z zad. 5.8 wynika:

K₂(z) =

kikizsin wT) z² — 2zcoswT) + 1'

A zatem:

kik D    kifaz sin uTi

* \^z) = --^ +

T z-D z² -2zcosvT_i + l’

(2)

(3)

(4)

T.

gdzie: D = e * ■

Po podstawieniu danych:

, , kik D    kikizsinir    hkD    , .

^K(’>-T7=D ⁺ z>-2,co^ ₊ ,-f(7^D)'    <⁵>

przy czym D = e~^l.

Zauważmy, że w transmitancji nie występują parametry członu oscylacyjnego. Wynika to z faktu, że okres impulsowania jest równy połowie okresu drgań własnych członu oscylacyjnego.

Warunek stabilności można otrzymać badając równanie charakterystyczne:

[1 + K (z)] (z - D) (z² - 2zcos7r + l) = 0,    (6)

czyli:

(z-D+ ^) (z + l)² = 0.    (7)

Ze względu na występujący w równaniu (7) podwójny pierwiastek z\$ = — 1 badany układ jest niestabilny.

Zadanie 5.12

Dla układu regulacji przedstawionego na rys. 5.28 podać wartości wielkości wyjściowej y w chwilach impulsowania oraz określić zachowanie się wyjścia układu między chwilami impulsowania, posługując się zmodyfikowaną transmitancją „z”, jeśli iv₀ = 1 (t). Przyjąć kik = T oraz zerowe warunki początkowe.

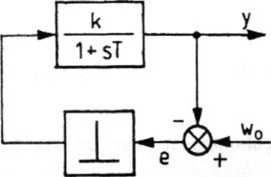
Rys. 5.28. Układ regulacji impulsowej bez elementu podtrzymującego

Rozwiązanie

Korzystając z wyników zad. 5.11 otrzymuje się:

K(z)

kik D T z-D'

(1)

Równanie charakterystyczne ma postać:

zD~^l -

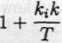
= 0.

(2)