275 (19)

274 Rozdział 5. Układy regulacji impulsowej

dla

musi zachodzić:

0 < kikTi <

Ti l-D 1 - D

kikTi <

D-%{l-D)’

2(1 + D)

l + D-2% {l-D)'

dla

D T l-D

< — <

l-D Ti 2 (1 - D) 2 (1 + D)

0 < kikTi <

1 + D-2£(1-D)’

natomiast dla

T 1 + D — >

T_t 2(1- D)

wystarczy, by

kikTi > 0.

W celu wyznaczenia y (nT;) obliczamy:

y (z) =    w (z) - ~^TH] A

^U l + K(z)^Wo{Z> l + kik[^-T^\

__kjk {z [T, - T (1 - D)} - 7)D + T (1 - P)}__z_

z² + z (-1 - D + kikTi - k_tkT (1 - D)] + D - k_{kTiD + kikT (1 - D) z - 1' Po podstawieniu danych:

ze^-1 + 1 - 2e~^ł z 0,368z + 0,264 z

(10)

(U)

(12)

(13)

(14)

(1)

(15)

Y(z) =

z² — z + 1 - e~^l z — 1 z² — z + 0,632 z — 1

(16)

W celu znalezienia y (nTi) zastosujemy odwrotne przekształcenie „z” (i twierdzenie całkowe Cauchy’ego):

y(nT_i) = ^_rJ^Y(z)zⁿ-'dz =

1 / 0,361 2irj f z² —

368z +0,264 z"

z + 0,632 z — 1

dz =

gdzie K jest konturem zamkniętym w płaszczyźnie zmiennej zespolonej z i obejmuje wszystkie punkty osobliwe funkcji podcałkowej, w tym przypadku jej bieguny.

Biegunami funkcji podcałkowej są pierwiastki jej mianownika, czyli:Natomiast wartości residuum w biegunie z* obliczamy jako:

res [Y(z)zⁿ-']_t=ti=(z-z_t)Y(z)zⁿ-\_=ir

A zatem

res[y(z)z»-U = ¥fS = ₁.

_rpę W M _rn-ll    _ 0,368(0,5+30,6181+0,264(0,5+j0,618)" _

res (X yZJ Z    J*=o,5+30,618 ^—    2(30,618)(0,5+3'0,618-1)

= 0,512e-’^167,8° (0,794)" (cosn51° + j sinn51°).

_rpc, W (₇n-11    - 0,368(0,5-j0,618)+0,264(0,5-j0,618)"

res [X (Z) z    J_z=0,s—j0,618 ^—    2(—y0,618)(0,5—yo.618—1)

= -0,512e-’^12,2' (0,794)" (cosn51° - j sin n51°).

Podstawiając otrzymane wyniki do (17) otrzymujemy:

y(nTi) = 1 - (0,794)" (cosn51° + 0,217sinn51°).    (18)

Zależność tę dla pierwszych pięciu kroków przedstawia rys. 5.33.

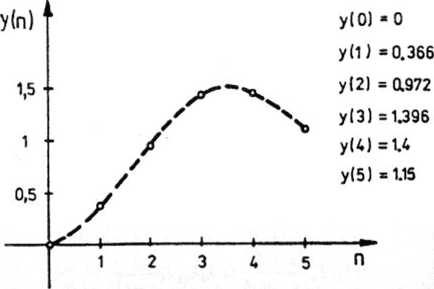
Rys. 5.33. Przebieg sygnału wyjściowego w chwilach impulsowania

Zadanie 5.14

Rysunek 5.34 przedstawia układ dwuwymiarowy regulacji impulsowej. Podać warunki stabilności, w przypadku gdy impulsatory pracują: a) synfazowo (próbkują w tej samej chwili czasu), b)niesynfazowo (momenty próbkowania różnią się o AT,). Okresy impulsowania i wzmocnienia obu impulsatorów są takie same.

Transmitancję obiektu przyjąć w postaci:

K(s) =

*11 *12 s \+sT J