283 (17)

282 Rozdział 5. Układy regulacji impulsowej

Transmitancję „z" układu otwartego można zapisać w postaci:

kuku *i2*i2

z — 1 z - 1

*ii *2i    *_t2*22

*11*21 *12*22 . Z — 1 Z — 1 .

(2)

Zatem równaniem charakterystycznym układu zamkniętego jest:

czyli:

(3)

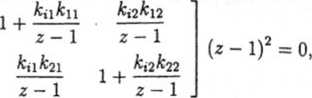
(z - 1 + kuku) (z - 1 + *12*22) - *12*11*12*21 = 0,

Z² + Z (*ll*il + *22*12 - 2) + (kuku - 1) (*22*12 - 1) - *12*11*12*21 = 0. Podstawiając:

ćł₀ = !> Aj = *11*11 + *22*12 - 2,    /ł₂ = (*11*11 - 1) (*22*i2 ~ 1) - *12*11*12*21

do warunków stabilności układu stopnia drugiego (wzór (9) zad. 5.13) otrzymuje

się:

*11*12 (*11*22 ^— *12 *21) > 0,

(4)

*11*11 "I" *12 *22    *11*11*12 *22 "t“ *12*11*12*21 ^ 0)

(5)

2 (*11*11 + *22*12) ^— (*11*22 ~ *12*2l) *il*i2 < 4.

(6)

Oznaczając

*11*11 — *ij *12*22 — *2

(7)

mamy:

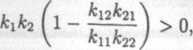
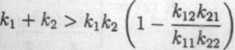
Podstawiając

k 12^21 k 11^22’

0)

mamy:

czyli:

<	■.Al aki-l	dla	ak\	> 1
k2 >	afci -1	dla	ak\	< 1

(10)

oraz

2 (fci + A2) — kik2<x < 4

zatem

dla	aki < 2	k2 <
dla	aki > 2	k2 >

2(2 - fci)

(U)

2 — afci

2 (2 — fci)

2 — aki

Na płaszczyźnie (k 1, fe₂) warunki (8), (10) i (11) przedstawiają obszary zakreskowane na rys. 5.37. Przyjęto przy tym, że 0 < a < 1, czyli sprzężenia skrośne w obiekcie są słabsze od głównych, oraz kuku > 0.

b) ImpuLsatory pracują niesynfazowo

W tym przypadku schemat zastępczy ma postać przedstawioną na rys. 5.38 (podobnie jak w zad. 5.14). A zatem

K(s) =

kn k\2 _c-sATi

^L s

^22

S

Transmitancja „z” układu otwartego przyjmuje postać:

K(z) =

kuku	ki2kn
2 — 1	2—1
kiik2i	^■2^22
.2—1	2 — 1 .

(12)

(13)