277 (20)

276 Rozdział 5. Układy regulacji impulsowej

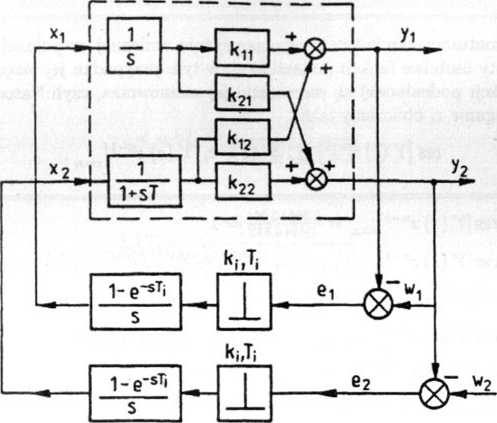
Rys. 5.34. Układ regulacji impulsowej dwóch zmiennych

Rozwiązanie

a) Praca synfazowa

Macierzowa transmitancja dyskretna układu ma postać:

gdzie:

K{z) =

K_n[z) K_n(z) K_n(z) K₂₂(z)

Ku (z) = kiZ {k_u [nTi 1 (nT«) - (n - 1) T,1 [(n - 1) Ti]]} =

= kikuTi-^; = kiknTr ¹

■(z-1)²    ^    *-l’

podobnie

K₂i (z) = kiknTi—^—, z - 1

natomiast zgodnie ze wzorem (25) z zad. 5.Ig):

K n (2) = kik_l2

(1)

(2)

(3)

1 - D z-D'	(4)
1 -D z-D’	(5)

przy czym

Ti

D = e~ + .

Równanie charakterystyczne układu zamkniętego ma zatem postać:

(*-l)(z-D)det [I + K(z)] = 0.    (6)

Po podstawieniu zależności (2), (3), (4), (5) do równania (6) otrzymujemy:

1 + kiknTi kiknjrB

(z — 1) (z — D) det co prowadzi do zależności:

{z-l){z-D)-1 + z — 1

z — 1 + kiknTi z — D + ki&22 (1 ^— D) ₂

z-D

— k_i kiknTi

= 0,

1 -D

(*-l )(*-£>).

= 0

+ z [kiknT) — 1 + kik22 (1 — D) — D\ +

+ k*k_uk22Ti (1 — D) — k*k\2k2\Ti (1 - D) + D — kik₂₂ (1 ^— D) — DkiknT = 0

(7)

Podstawiając

A₀ — 1, A\ — kiknTi — 1 + kik22 (1 ~ D) — D

A2 = kJkiikiiTi (1 — D) — k?kuk2\Ti (1 — D) + D — kik₂₂ (1 — D) — DkiknT,

do warunków stabilności (wzór (9) z zad. 5.13) otrzymuje się:

kik_nTi + kik₂₂ (1 - D) + kukali (1 - D) - kfknknT (1 -D) +

—kik22 (1 — D') — DkiknTi > 0,

(1 - D) - kfknknTi (1 - D) + k?k₁₂k₂iTi (1 - D) + kik₂₂ (1 - D) + kik_nTiD > 0, 1 - kiknTi + 1 — fcj/c22 (1 — D) + D +    (1 — D) — k?k_uk_2lT (1 - D)

+D — kiki2 (1 - D) — kiknTD > 0,

czyli

ki (1 — D) Ti [ku + ki (knk22 — ki2k2i)] > 0,    (8)

(1 — D) [l + k?Ti (ki₂k₂i — kuk22) + kik22] + kiknTD > o,    (9)

(1 +    D) (2 - k,kiiTi) + (!-£)) kj [-2k₂₂ 4- k_{T (knkw - ki₂k₂i)j > o    (10)