279 (19)

278

Rozdział 5. Układy regulacji impulsowej

278

k_i(Ti

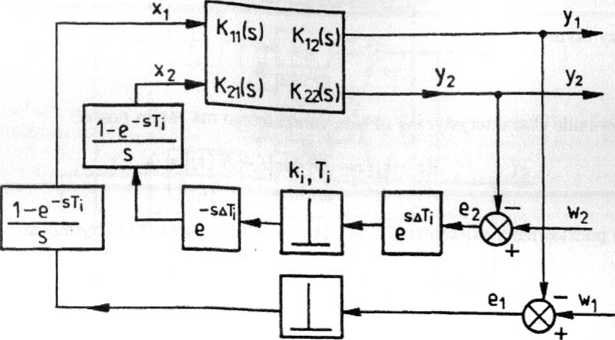
Rys. 5.35. Schemat zastępczy układu niesynfazowego

b) Praca niesynfazowa

Można ten przypadek traktować tak, jak gdyby sygnał z drugiego impulsatora względem pierwszego był opóźniony o AT,(0 < A < 1). Schemat zastępczy układu ma wówczas postać przedstawioną na rys. 5.35.

Wpływ opóźnienia kompensuje się elementem przyspieszającym o AT,, aby schemat układu był równoważny układowi wyjściowemu.

Transmitancja operatorowa części ciągłej będzie miała w tym przypadku postać:

K₀(s) =

f (1 - e~^sTi) e

-5 AT,

*12

s(1+jT)

_*22_

s(l+*T)

(1

e *^T') e"

(1 - e-‘^T0

A zatem transmitancja dyskretna będzie miała postać:

'*11 W *12 W

*M =

gdzie podobnie jak w punkcie a):

*11 (^z) ⁼

*21 (^z) *22 W 1

*22 (^z) = *i*22

Z — 1 *

I-D

sAT,

(U)

Natomiast:

Ponieważ

z-D

K_u (z) = Z[k_iku (nTi)}.

ku (t) = ku { (l - e-^) 1 (t - ATj) -

_    !(<-(! +A) T,]},

więc

*12 (nli) = *12 { (l - e-'"-^A^) 1 [(n - 1) T] - (l -    1 [(n - 2)Tj}

Zatem zgodnie ze wzorem (15) z zad. 5.1, d) i twierdzeniem o przesunięciu:

#12 (z) = *i*i2

(L - D) z + D (1 - L) L{z-l)(z-D)

(l -    = *i*12-

(L-D)z + D(l-L)

Lz {z — D)

(12)

gdzie L = e ^A^ = D^A. Podobnie

#21 (z) = Z [*i*21 (nT)],

*21 (t) = *21 {(t + AT,) 1 (t + ATi) — [t — (1 — A) Ti] 1 [t - (1 - A) T]},

skąd

*2i (nT) = *2i {(n + A) T 1 (nTi) - (n - 1 + A) T,1 [(n - 1) T,]} =

= *21 {nTi (nT,) - (n - 1) Tl [(n - 1) T,] + AT, [1 (nT) - 1 (n - 1) T]} .

A zatem

#21 (z) — *2lT*i

+ A

= *21 Tiki

1 +A

z - r

(13)

Wyznacznik det [/ + T (z)] jest w przypadku b) określony następująco: det

1 + #n (z)    #12 (z)

#21 (2)    1 + #22 (z)

— det

1 . L L 'T* 1 L. 1- (L-D)t + D(l-L) l +    Lz(ż-D)

*2lT,*i*^    l + fci*₂₂^§

. _ t-l+fcfcnTi z-P+fcit₂2(l-J)    L2Ł. ł >T l(t.-Q)«+P(l-Ł)l(l+A)

"    z-1    z-D    »i»12*21 Z, L*(ł-D)(*-1)

Równanie charakterystyczne ma postać:

z³ + z² [*i*nT ^— 1 + *1*22 (1 ^— D) — D] +

1 +A

*,²*n*22Ti (1 - D)+D-k_xk₂₂ (1 - D)-Dk_lk_nT_x-k²ik₁₂k₂₁T_x—— (L - D)

z+

- *,²*i2*2iTiT (1 - L) = 0. (14)

Podstawiając:

A₀ = *i*nT - 1 + *i*22 (1 - D) - D,

Ai = k²k_nk₂₂T_x (1 - D) + D - *,*22 (1 - £>) - D*j*nT - *,²*i2*2iT[L - D), A₂ = -kfk₁₂k₂₁TiD(l-L)^,