263 (19)

262 Rozdział 5. Układy regulacji impulsowej

gdzie:

(3)

D = e~%, L = e~ł.

Transmitancja dyskretna ma zatem zgodnie ze wzorami (17) i (18) z zad. 5.1 postać:

K(z) = k%

D(l~L)

L(z - D)

(4)

Jeśli założy się, że S_n = const przy 7 —> 0, to otrzymuje się k, = k[7 = const. Wówczas

lim K (z) = lim 7—*0    7 ■'

■    ° ń \-^k% =

o z - D e~ł

e

D e?

= lim -— —

7—>o z — D

I. 1 k₀k{ —kik₀ -

z - D

(5)

Wynik ten zgodny jest z transmitancją dyskretną układu, w którym występuje impulsator idealny (zad. 5.1e).

Jeśli przyjąć, że 7 —> Ti, to:

(6)

kik₀ D (1 - D) _ kik₀1 - D ~ T D(z-D) ~ ~T~z-D'

Wyrażenie (6) zgodne jest z transmitancją dyskretną układu z impulsatorem idealnym i członem podtrzymującym zerowego rzędu (zad. 5.Ig), przy czym w mianowniku występuje tu T, wynikające z faktu, że k, reprezentuje pole impulsu o szerokości 7), a nie pole impulsu idealnego (o szerokości 7 —> 0).

Schemat blokowy układu zamkniętego jest przedstawiony na rys. 5.23.

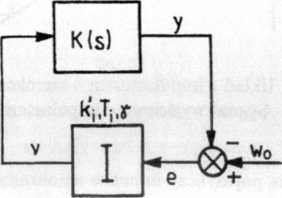
Rys. 5.23. Schemat blokowy układu zamkniętego z impulsatorem o szerokości impulsu 7

Stabilność zbadamy na podstawie równania charakterystycznego:

Otrzymujemy więc:

z-D + fc'fc₀- (1 - L) = 0.

Jb

(8)

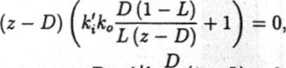
Aby układ był stabilny, pierwiastek Z\ równania musi spełniać nierówność:

M < 1.

czyli

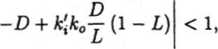
(9)

W przypadku gdy 7 —> T_it wynik ten odpowiada (5) z zad. 5.5.

Zadanie 5.10

W układzie przedstawionym na rys. 5.24 impulsator liniowy generuje impulsy o okresie impulsowania T; = 1 [s], szerokości 0 < 7 < 1 i wysokości proporcjonalnej do uchybu w chwili impulsowania. Podać warunki stabilności układu, zakładając, że k[ = ki7 = const. Zbadać zależność k[, zapewniającego stabilność układu, od 7.

1

V

1 + ST

Rys. 5.24. Układ impulsowy z impulsatorem o modulowanej wysokości impulsu Rozwiązanie

Rysunek 5.25 przedstawia przykładowy przebieg sygnałów:

x (t) i v (t) dla n < t < n + 1    (T< = 1 [5]).