287 (17)

286 Rozdział 5. Układy regulacji impulsowej

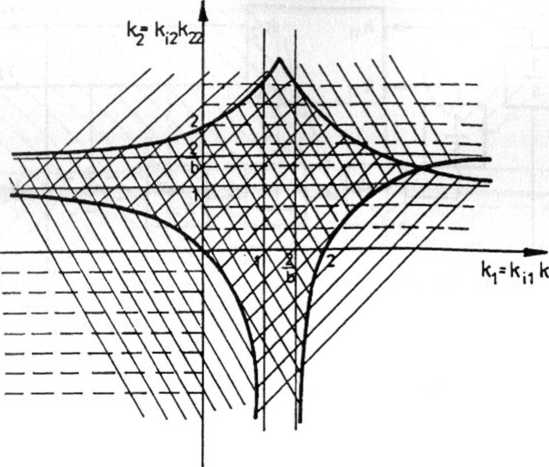
Rys. 5.39. Obszar nastaw dopuszczalnych na płaszczyźnie (k_u k₂) w przypadku niesynfazowej pracy impulsatorów

Jeśli podobnie jak w punkcie a) przyjmiemy 0 < A:₁₂fc2i < kuk^, to

2 > 6 = 1 + rp-rp- > 1 *11*22

Ilustracją warunków (19), (20) i (21) jest rys. 5.39.

W przypadku braku sprzężeń skrośnych k\₂k₂\ — 0 obszary dopuszczalnych nastaw dla impulsatora pracującego synfazowo i niesynfazowo pokrywają się. Wówczas bowiem a = b = 1 i parametry dopuszczalne określone są nierównościami

0 < ki < 2,    0 < k₂ < 2.

W przypadkach przedstawionych na rysunkach 5.37, 5.39, tzn. jeśli:

0 < k\₂k₂\ < k\\k₂₂

obszar dopuszczalnych nastaw k\k₂ przy pracy synfazowej jest mniejszy niż obszar dopuszczalnych nastaw przy pracy niesynfazowej.

Jeśli -k_nk₂₂ < k_nk₂i < 0, wówczas a > 1, natomiast 0 < b < 1, zatem obszar dopuszczalnych nastaw wzmocnień regulatorów przy pracy synfazowej ulegnie zwiększeniu, natomiast dla pracy niesynfazowej - zmniejszeniu.

Natomiast w przypadku, gdy k\₂k_2l > k_uk₂₂, obszar dopuszczalnych nastaw na płaszczyźnie (ki,k₂) leży w drugiej i czwartej ćwiartce, tzn. jeden z impulsatorów powinien mieć ujemne wzmocnienie.

Zadanie 5.16

W podanym na rys. 5.40 układzie impulsator generuje impulsy idealne, przy czym pole powierzchni n-tego impulsu opisuje zależność:

S_n = k_t [e (nT^ + e ((71-1)7))]

Wyprowadzić warunki stabilności układu.

y

kiJi

Rys. 5.40. Układ impulsowy zawierający impulsator z pamięcią Rozwiązanie

Część ciągła układu ma transmitancję:

*(») = ;.    (i)

Odpowiada jej transmitancja dyskretna:

K₀(z) = kkij^-.    (2)

Ponieważ impulsy podawane na część ciągłą mają pole proporcjonalne do {e (nT,) + e [(n — 1) 7)]} a więc zgodnie z twierdzeniem o przesunięciu:

y (z) = K₀ (z) (l + ^ £ (z) = kki-^-Eiz),    (3)

czyli transmitancja „z” układu otwartego jest:

*<‘> = “‘1^    <⁴>

Równanie charakterystyczne układu zamkniętego można zapisać zatem w postaci:

z² - z + kk_t (z + 1) = 0,

z² + (kki - 1) z + kk_t = 0.    (5)

Korzystając z warunków stabilności (wzór (9) z zad. 5.13) otrzymuje się:

1 + kki — \ + kki > 0.

1 — kki > 0,

1 — kki + 1 + kki > 0.

Czyli

0 < kki < 1. (6)