289 (18)

288 Rozdział 5. Układy regulacji impulsowej

Zadanie 5.17

Wyprowadzić warunki stabilności dla układu o schemacie przedstawionym na rys. 5.41, w którym impulsator generuje impulsy o kształcie trójkątnym jak na rys. 5.42 i wysokości proporcjonalnej do uchybu w chwili próbkowania.

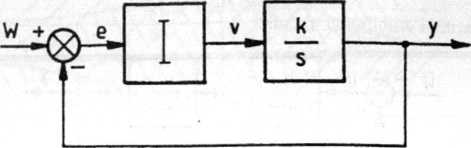
Rys. 5.41. Układ impulsowy - schemat blokowy układu

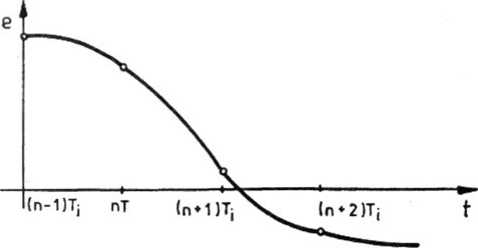
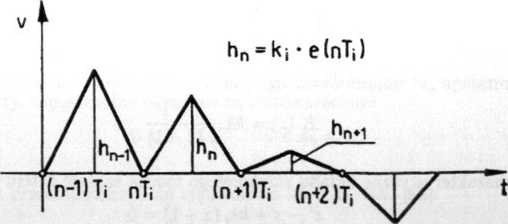
Rys. 5.42. Układ impulsowy - kształt impulsów generowanych przez impulsator

Rozwiązanie

Po podaniu na część ciągłą (element całkujący) pojedynczego impulsu trójkątnego otrzymuje się na wyjściu sygnał proporcjonalny do pola tego impulsu:

Vn — ł/n—1 4" hPn-

A więc odpowiedź części ciągłej na pojedynczy impuls ma postać taką, jakby na wejście tego elementu podany był impuls idealny o polu równym polu trójkąta:

(1)

Pn = \hnTi = ^l-We (nTi).

Zatem impulsator w układzie można zastąpić impulsatorem idealnym o wzmocnieniu

ijicT 2'W-* x*

Transmitancja „z” dla układu otwartego ma wówczas postać:

K(z)

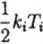
k

z — 1

Pierwiastek równania charakterystycznego

^{1 +} Ś*'^Tvh

= 0

(2)

ma wartość:

(3)

(4)

zi = ^k,kTi - 1.

A więc warunek stabilności określa zależność:

0 < kik <

Zadanie 5.18

W układzie regulacji impulsowej przedstawionym na rys. 5.43 impulsatory liniowe generują impulsy trójkątne (rys. 5.44) o wysokości proporcjonalnej do wartości uchybu podawanego na impulsator w chwili impulsowania i szerokości równej połowie okresu impulsowania Ti. Zakładając, że macierzowa transmitancja obiektu ma postać:

K(s)

kie~^,Tl s	0	0
k 21	k2e~^,Tt	0
1 + sT2\	s
^31	ki2	k3e-^,T>
1 + sTn	1 + sT$ 2	s

(1)

gdzie: 0 < T_x < 0,5T1,    0,5T< <T₂< T_it Ti = Ti, podać warunki stabilności układu.