271 (18)

270 Rozdział 5. Układy regulacji impulsowej

Po podstawieniu danych otrzymujemy:

z = 0.

Widać więc, że zamknięty układ regulacji jest stabilny. Ponieważ:

(3)

(4)

W₀(z) = Z[ !(»)] = TT?

więc

_rr-_v.. W₀{z)    _ żj    z(z-D)

^W 1 + K(z) 1 + ^JL (z - 1) (z - D + ^D)

Po uwzględnieniu danych otrzymuje się:

E(z)

z (z - D) (z - l)z

z D z — 1 z — 1 *

(5)

o e(nTj) * y(nTi)

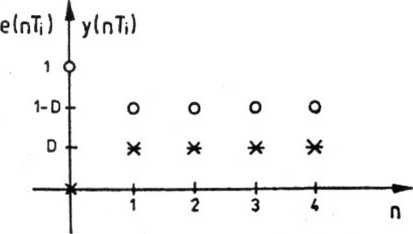
Rys. 5.29. Przebieg uchybu i sygnału wyjściowego w chwilach impulsowania

Zatem uchyb w chwilach impulsowania ma wartości (rys. 5.29):

e (nTj) = 1 (nTi) - Dl [(n - 1) 7)].    (6)

Aby określić przebieg y pomiędzy chwilami impulsowania, posłużymy się zmodyfikowaną transformatą „z”. W tym celu wprowadzimy w torze głównym układu opóźnienie czasowe o A Ti, którego wpływ kompensujemy w torze sprzężenia zwrotnego (rys. 5.30), przy czym 0 < A < 1.

Zmodyfikowana transformata „z” sygnału wyjściowego ma postać (zgodnie z rys. 5.30):

Y(m,z)

K (m, z) W„ (z) 1 + K (z)

gdzie: m=l-A,aif(m,2) jest zmodyfikowaną transmitancją układu otwartego.

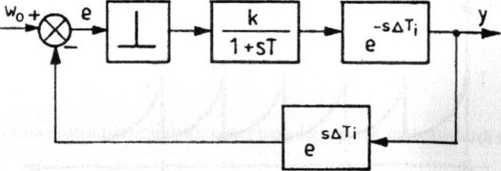
Rys. 5.30. Schemat blokowy do badania przebiegów y w dowolnej chwili

K (m, z) obliczyć można ze wzoru:

OO

(m, z) = *<£>[(«-A)

w rozważanym przypadku:

'« - A i Tl r=

T

A zatem

n=0

K[(n- A) Ti] = L1 [(n - A) T,\.

(8)

K (m,z) = ki^2    ?^)T i [(_n - A)T<] z ⁿ =

= A:* — |e r Z +e r _er

= __

^<ę,'T^C    , Zi

2    1 - Z^_1e r

— nm__L_

T z — D'

ii _o    U-W łT;

e r z + e 5^ e t z

-■]*

(9)

gdzie

D = e~T.

A zatem:

nm 1

¹ + T i-D ^Z 1

(10)

Po podstawieniu danych:

Y (m, z) = D"

z — 1

(U)

Wartość sygnału wyjściowego w dowolnej chwili można zatem obliczyć jako: y (m, nT,) = D^m 1 [(n - A) 7J] = D^m 1 [(n - 1 + m) T,].

(12)