249 (21)

248 Rozdział 5. Układy regulacji impulsowej

Zadanie 5.2

Zbadać stabilność układu regulacji impulsowej podanego na rys. 5.9 oraz znaleźć przebieg uchybu regulacji przy sygnale wiodącym w„ (t) = 1 (t), przyjmując dane:

Ii-l W

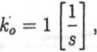
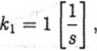
oraz zerowe warunki początkowe.

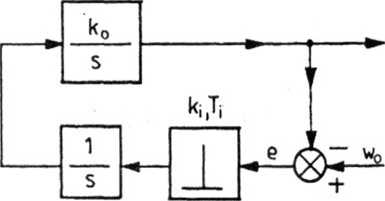
Rys. 5.9. Schemat blokowy układu regulacji impulsowej z zadania 5.2

Rozwiązanie

Transmitancja części ciągłej układu ma postać :

k„

(1)

(2)

^K (s) =

Odpowiedź impulsowa dla tej transmitancji jest:

k (t) = k₀tl (t).

A zatem

k (nTi) = k₀nTi 1 (nTj)

Transmitancja ”z” układu otwartego ma zatem postać:

K(z) = k₀k_iT_i-^-3.

(z - 1)

Równanie charakterystyczne układu zamkniętego:

(z-l)²(l + tf(z))=0,

czyli

gdzie:

A₀ = 1, A\ = k₀kiTi - 2, A₂ = 1.

Podstawiając

z =

w + 1

ty - 1

otrzymuje się

ty² (A₀ + Ai + A₂) + ty2 (A₀ — A₂) + (A₀ — Ai + ^2) ⁼ 0

(5)

czyli

w²k₀kiTi + 4 — k₀kiTi = 0.

Na podstawie kryterium Hurwitza stwierdzamy, że układ nie jest stabilny, przy czym dla k₀kiTj < 4 układ znajduje się na granicy stabilności, a dla k₀k_tT_x > 4 układ jest niestabilny.

W celu znalezienia przebiegu uchybu znajdziemy pierwiastki równania charakterystycznego (4):

-k₀k_{Ti + 2 ± ^kjk?T? - Ak₀kiTi zi,2 =-2-

Podstawiając dane mamy:

^zi = \ (i -    3) ,    22 = ^ (l + jV5) .    (7)

Łatwo zauważyć, że |zi| = |z₂| = 1 potwierdzając, że układ jest na granicy stabilności. Transformata „z” dla uchybu regulacji ma postać:

E(z) =

W₀{z)

1 + K(z)'

Transformata „z” sygnału wiodącego jest równa:

z

W₀(z) =

z- r

a zatem

E(z) =

2(2-1)

Z — Z\ z

Podstawiając dane otrzymuje się:

(z - 1) (kokrTij^ + 1) ^{z2 + z} (Wtfł - 2) + 1

Ai A₂ I .    2 _a z

+-— \=Ai-+ A₂-

-22 J ‘ “

Z — Zi z — z₂

Ai ₊ A₂

- 1

Z² — Z + 1 Z — Zl Z — z₂

(8)