235 (24)

234 Rozdział 4. Ocena przebiegów w układach regulacji ...

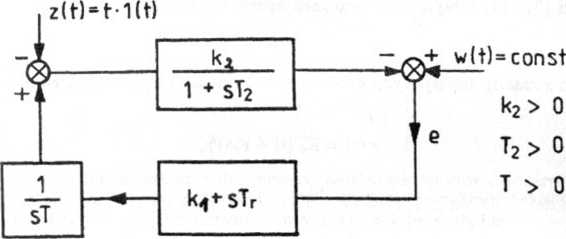
Rys. 4.41. Schemat blokowy układu z zadania 4.26

Rozwiązanie

Równanie charakterystyczne badanego układu jest następujące:

S^T₂T + 5 (T + k₂T_r) + k\k₂ ⁼ 0.    (1)

Warunek aperiodyczności przyjmuje postać:

A = (T + fc₂T_r)² - 4k_xk₂T₂T > 0.    (2)

Podobnie jak w zadaniu 4.25 można pokazać, źe dla t > 0 uchyb e (f) jest równy zaburzeniu wprowadzonemu do układu przez sygnał z (t).

e (t) = e_t (f), t > 0.

Transformata operatorowa sygnału e_z (t) jest określona następująco: -^(s)    k₂T

(3)

E,(s) =

1+372

1 +    s {s*T₂T + s(T + k₂T_r) + fafe]'

(4)

Wartość ustalona sygnału e (t) jest równa:

(5)

e«, = lim [sE, (s)] = —.

3—>0    K\

Przy spełnionym warunku aperiodyczności (2), uwzględniając zależności (3), (4), (5) otrzymujemy:

00 00

j = J |e (t) - Cool di = J [eoo - e_z (t)] dt = y - E_t (s)] ^ =

1 \T

k₂T

S [fcl S^T₂T -+• 3 (T -h k₂T_T

_]    ₌ T(T + k₂T_r)

r) +    _J=0    ^2^1

(6)

Ponieważ wartość wskaźnika jakości maleje wraz ze wzrostem wzmocnienia Aą, więc po uwzględnieniu ograniczenia na ki wynikającego z warunku aperiodyczności otrzymujemy:

•Anin —

\6k₂T³T₂ {T + k₂T_rmtx)

3'

(7)

Przy spełnionym warunku aperiodyczności (2) najmniejszą wartość przyjętego wskaźnika jakości otrzymuje się nastawiając największą osiągalną w regulatorze wartość T_r = T_rmax oraz wzmocnienie ki na wartości:

(8)

I

. _ (T + k₂T_rmix)² 1 4T₂Tk₂ '

Zadanie 4.27

Dany jest układ regulacji (rys. 4.42). Określić wartość wzmocnienia ki zapewniającą

CO

uzyskanie minimalnej wartości całki / e⁷dt dla zerowych warunków początkowych y (0),

o

v (0) oraz wymuszenia w (t) = 41(t). Jaki będzie wówczas stopień oscylacyjności układu?

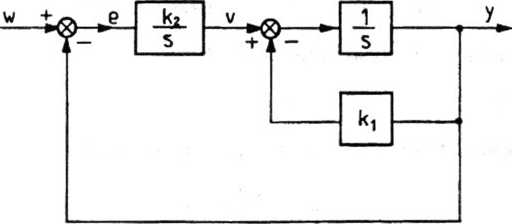
Rys. 4.42. Schemat blokowy układu z zadania 4.27

Rozwiązanie

Jeśli wyrażenie na e (s)

przedstawimy w postaci: c(s)

e(s) =

d(s)’

przy czym

c(s) = 5I^C*^S*>

k=0 n

d(s) = ^2d_ks^k, n>m,

*=o

to w przypadku, gdy d (s) ma zera tylko w lewej półpłaszczyźnie, otrzymujemy:

J e²dt = <

o

cl

2 <Mi>

2dod\di *

(Ądod\+(c\-1c*C2)dods+cld2di 2dods(—dod\+d\d2)    ’

Tl = 1 Tl = 2

n = 3

(1)

(2)

(3)

(4)

i