227 (24)

226 Rozdział 4. Ocena przebiegów w układach regulacji ■ ■ •

Uwzględniając związki (4), (5) oraz (1) możemy określić wartość ustaloną uchybu przed wprowadzeniem zaburzenia:

e(0-)=U_tad-^M_R    (16)

Wprowadzając do zależności (13), (14), (15) oraz (16) dane liczbowe otrzymujemy:

(17)

(18)

(19)

i_w(<) — [5(l — e^_201t) + 4e”^201t] l(t) [A], e(O-) =0,4[V],

e (t) = (19,6e~^201t + 0,5) 1(<)    [V]

Przebiegi czasowe i_w (t) oraz e (t) przedstawiono na rys. 4.35.

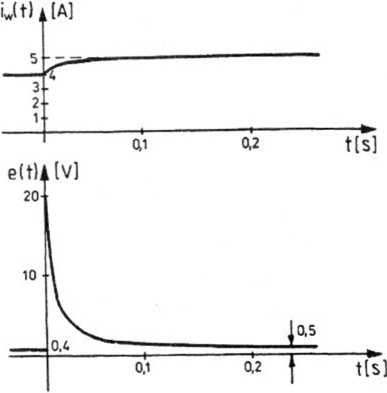
Rys. 4.35. Przebieg prądu wzbudzenia i_w (t) oraz uchybu e (t) w układzie z rys. 4.34

Zadanie 4.23

Dla układu o danym schemacie blokowym (rys. 4.36) zbadać stabilność i podać postać stabilnego elementu o transmitancji k_p (s), aby zakłócenie zi (t) nie oddziaływało na wielkość wyjściową obiektu.

Macierzowe transmitancje obiektu i regulatora określona następująco:

	[*> ;i		' Ui '
	. 3(3 + 1) 3 .		. ^ .

(1)

‘ Y_t

.Y,

	l + \ 0		El ‘
	kp (s) 1 + -		. ^ .

. X₂

t/₁₌ X, + Zi

l/₂= x₂

r

OBIEKT

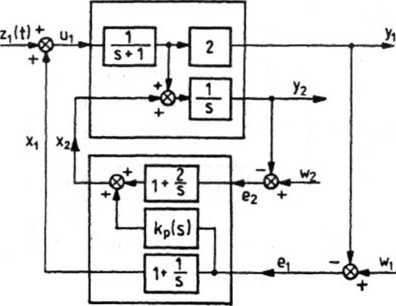
Rys. 4.36. Schemat blokowy układu z zadania 4.23

Rozwiązanie

Układ jest stabilny, bo równanie charakterystyczne

(s + l)(5 + 2)(s² + s + 2) =0    (3)

ma pierwiastki o częściach rzeczywistych ujemnych. Ponadto widać, że ze względu na stabilność oba obwody regulacji są niezależne, pomimo regulatora o strukturze niediago-nalnej.

Na podstawie schematu blokowego można narysować ideowy schemat przechodzenia sygnałów w układzie (rys. 4.37), przyjmując dla uproszczenia następującą postać transmi-tancji obiektu i regulatora:

K_u (a) 0 K₂\ (s) K₂₂ (s)

K_rl(a) 0 _L k_p (s) Kri (s)

Na rys. 4.37 widać, że sygnał y₂ nie zależy od Zj, gdy zachodzi warunek:

K₀(s) =

K_r(s) =

(4)

(5)

(6)

K_n (s)-K_n (s)k_p(s)K₂₂(s)=0,

czyli

Y(s) = K,

UW

nw

= Ko (») •

Z(s) =

Zł W '

o

i