223 (29)

222 Rozdział, 4. Ocena przebiegów w układach regulacji ■. •

Zadanie 4.21

W układzie z zadania 4.20 (rys. 4.30) silnik obciążono momentem m₀l{t). Obliczyć uchyb regulacji w stanie ustalonym pochodzący od tego momentu. Czy uchyb ten można zmniejszyć przez wprowadzenie na wejście wzmacniacza tachometrycznego ujemnego sprzężenia zwrotnego?

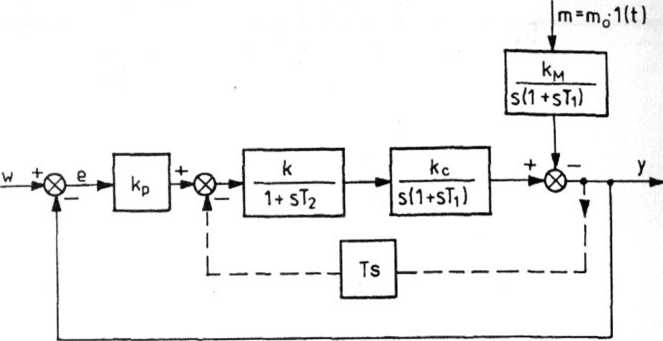
Rys. 4.33. Schemat blokowy układu śledzącego

Rozwiązanie

Na schemacie blokowym układu (rys. 4.33) linią przerywaną zaznaczono tachometryczne ujemne sprzężenie zwrotne.

Uchyb pochodzący od momentu obciążenia w układzie bez sprzężenia tachometrycznego

wynosi:

(1)

k_M{l + sT₂)M{s) s³T,T₂ + s² (Ti + T₂) + s-

M{s) =

m₀

(2)

W stanie ustalonym:

e_x = lim^ [sE (s)] = lim^

m₀_kj\ą (1 -t sT₂)_

s s³TiT₂ + s² (Ti + T₂) + s -f- kpkk_c

k_pkk_c

Stan ustalony w układzie wystąpi tylko wówczas, gdy układ jest stabilny. Zgodnie ze wzorem (2) zad. 4.20 układ jest stabilny, gdy

k <

Ti+T₂

T\T₂k_pk_c

Zatem w układzie bez sprzężenia tachometrycznego:

^00 **

Tn₀kMT\T₂

T,+T₂

(4)

W układzie z ujemnym tachometrycznym sprzężeniem zwrotnym uchyb pochodzący od momentu obciążenia wynosi:

E{s) = M(s) = M (s)

w

_s (1 4- cT, 1 1 i kkrTs__,__k_vkk_c

⁵' ⁺    l,1+ s(\+sT₂)(i+>t₁) ⁺ ^i+jTjKi+jT,)

k\i (1 + sT₂)    _

s³T₂Ti 4- s² (Ti +T₂) + s( 1 + kk_cT) 4- k_pkk_e W stanie ustalonym po podstawieniu związku (2) otrzymuje się

eoo = lim s—>0

(1 + sT₂)

s s³T\T₂ + s² (Ti + T₂) 4- s (1 + kk_cT) 4* k_pkk_c

m₀k_M kpkk_c'

(5)

(6)

a więc wynik identyczny jak (3).

Inny jest jednak warunek stabilności. Równanie charakterystyczne ma w tym przypadku

postać:

s*T\T₂ 4" s* (Ti 4" Ti) 4- s (1 4- kk_cT) 4" k_pkk_c — 0,

a zatem układ jest stabilny, gdy:

(7)

(Tj 4- T₂) (1 4- kk_cT) — kpkk_cT\T₂ > 0,

czyli

k [(Ti 4- T₂) k_cT — k_pk_cT\T₂\ 4- Ti 4- T₂ > 0.

Jeśli

T <

kpTT₂ Ti 4- T₂’

to

k <

Ti 4- T₂

k_c[kpTiT₂-(Ti+T₂)T}

(8)

(9)

m₀k_MTiT₂ (    T(Ti+T₂)\

⁶⁰⁰    T,+T₂ V¹ kpTiT₂ )

a jeśli T >    , to układ jest stabilny dla każdego k (dodatniego) i uchyb w stanie

ustalonym można zmniejszać do dowolnej wielkości.