231 (26)

230 Rozdział 4. Ocena przebiegów w układach regulacji ...

Zatem musi być spełniony układ równań:

hi (®) + hi (s) = 0 —C₀/n (s) + (C20 — C„) lii (s) = 0

Stąd:

(7)

~hi (s) = ^22 («)    1

ki (^s) ⁼    (^s) 1

Widać, że w zależności od wybranego punktu pracy obiektu transmitancje korektora

są różne.

Dla danego z zad. 2.14 punktu pracy mamy:

(8)

I12 (s) = -la (s) \ hi (s) = \h\ (*) J

Dla elementów korektora leżących na przekątnej głównej L (s) można przyjąć dowolne postaci transmitancji.

Weźmy:

hi (5) = 1,    (9)

la (s) = 1,

zapewniając własności dynamiczne układu w torach głównych takie same jak w układzie bez odsprzęgania.

Wtedy na podstawie zależności (8) mamy:

L(s) =

1

1

L 2

(10)

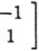
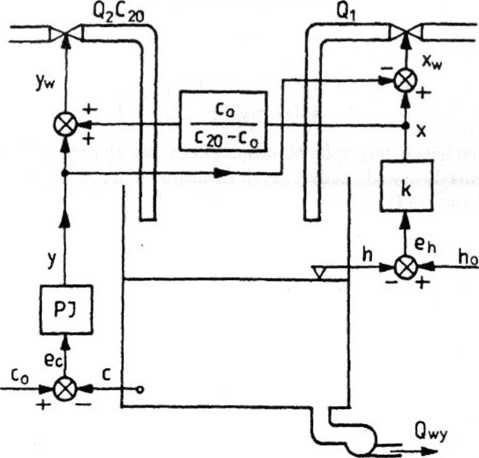
Realizację powyższego sposobu odsprzęgania przedstawia rys. 4.39.

W celu określenia warunków stabilności dla układu z korektorem o transmitancji L (s) zbadamy równanie charakterystyczne układu, zapisując transmitancję układu otwartego w postaci:

(U)

G₀(s) = K_a(s)K_r(s),

gdzie: K_r (s) - transmitancja macierzowa regulatora dana zależnością (14) zad. 2.14, natomiast K_a (s) dla L (s) opisanego macierzą (10) i danych z zad. 2.14 jest następująca:

K_a(s) =

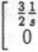
0

3

1+* .

(12)

Zatem równanie charakterystyczne ma postać:

(s + 15) [s²T_cV + s (T_CV + 3T_c) + l] = 0,    (13)

a więc układ odsprzęgnięty jest stabilny dla dowolnych wartości T_c oraz V (dodatnich).

Rys. 4.39. Schemat układu regulacji stężenia i poziomu z uwzględnieniem korektora L (s) b) Przez K_ar (s) oznaczmy transmitancję regulatora umożliwiającego odsprzęgnięcie.

Przyjmując, że w torach głównych regulatory są takie jak we wcześniej rozpatrywanym przypadku a) K_ar (s) można napisać jako:

Kar (s) =

' 10	ki (s)
M«)	v (^1 +

(14)

Zatem transmitancja układu otwartego ma postać:

<?.(») =

Qwyo A}XqS

— [10 +(a)]

[—10c_o + (C20 - c₀) k₂ (s)]

_6_

(15)

As

Aby zachodziła autonomizacja, elementy G₀ (s) nie leżące na przekątnej głównej powinny się zerować, czyli

(16)

‘■w⁺Kⁱ⁺A)'^0,