24

obliczymy ze znanego już wzoru (40):

Następnie z punktu B zataczamy rulet]$(||łuk o promieniu równym y i przesuwając się po nim z pryg||§itern znajdziemy taki punkt M, aby AM było prostopadłe do-ĘĘm. Wyznaczywszy w ten sposób styczną AM, wystawiamy Ś$|pniej prostopadłą w punkcie A otrzymując szukany kierunek przekroju normalnego. Gdy odcinek AM jest krótszy niż przymiar (taśma), wówczas możemy obliczyć jego długość

x = yc⁸—y²

i znaleźć punkt M jako przecięcie' łuków zatoczonych promie-

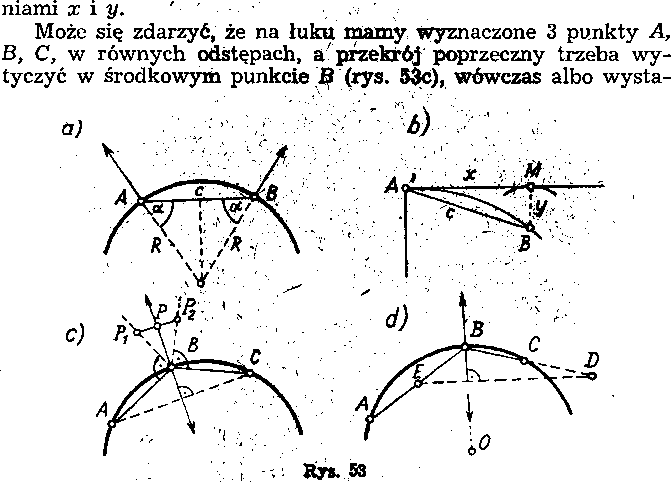
wiamy prostopadłą ze środka cięciwy AC, albo budujemy dwa kąty proste ABP_X i CBP₂, na ich ramionach odkładamy dowolne, lecz równe odcinki BP_X i BP₂, a następnie połowimy odcinek P1P2 otrzymując punkt P. Prosta BP wyznacza szukany przekrój poprzeczny.

Jeżeli 3 dane punkty A, B, C nie leżą na łuku w równych odstępach (rys. 53d), to na prostej BA odmierzamy odcinek BE = = BC, na przedłużeniu prostej BC odmierzamy odcinek BD = BA, a następnie przez punkt B tyczymy prostopadłą do ED, która

| 1 przejdzie przez środek okręgu O i wyznaczy kierunek poszuki-wanego przekroju poprzecznego. Dowód można przeprowadzić rysując taką samą konstrukcję symetrycznie względem OB.

** W jytoP aczanie w terenie promienia luku 1e j J9peg o

Ńajpro^ferm sposobem wyznaczenia promienia danego luku jest j3dmia|ppeciwv i strzałki wystawionej w jej środku. Przy-. bliżoną zalRjlość między tymi dwiema wielkościami i promie-iJPimem daje pf^r (43). Zależność ścisłą wyprowadzimy na podsta-|||k wie rysunł||r$4. Odcinek AB = c oznacza na nim cięciwę, ED — s

//

v ^v / -'C-'

Rys. 54    •'

^ strzałkę należącą dó tej cięciwy, a odcinek AD J* Ci cięciwę '_vy\o rozpiętości dwa razy niniejszej. Z podobieństwatrójkątów kf? i ADF wynika    ‘    -«    . "'^y '

2R

8 =

fc¹' lecz z trójkąta prostokątnego ADE otrzymamy

la zatem

s²+-

s =

2 R    ’

&

97

g»7 Pomiary specjalne cz. I