40

dziemy z wzorów (57) i (60). Współrzędne X i Y dowolnego punktu klotoidy, a więc i punktu P, obliczymy z wzorów (61).

Aby obliczyć pozostałe wielkości, mogące się przydać w praktyce, przedłużmy wstecz następujący po klotoidzie łuk kołowy i z jego środka S opuśćmy prostopadłą na styczną główną. Kąt między tą prostopadłą i promieniem krzywizny w punkcie P

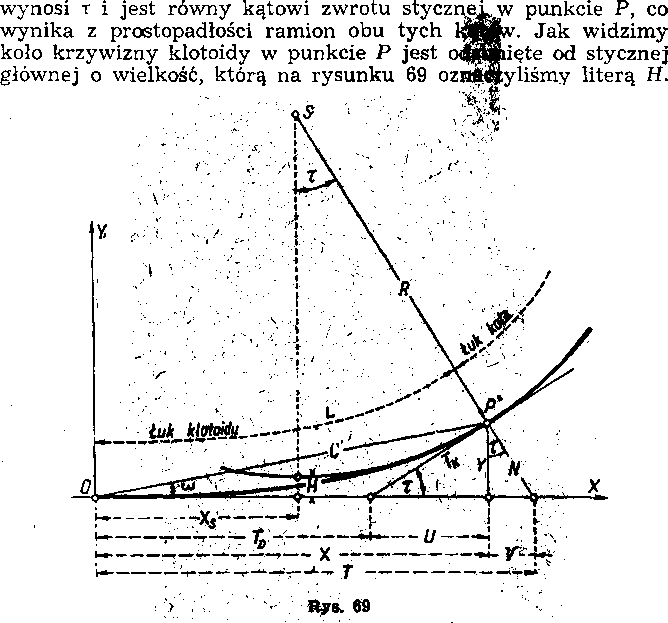
Prostopadła do stycznej, wystawiona w punkcie styczności z krzywą, nazywa się, jak wiemy, normalną, lecz tu będziemy normalną nazywali tylko odcinek tej prostopadłej zawarty między rozpatrywanym punktem P i styczną główną. Oznaczamy go literą N.

Po tych wyjaśnieniach, znając już wielkości wchodzące do wzorów (57)-j-(60), a z tablic — współrzędne X i Y punktu P, w którym klotoida styka się z łukiem kołowym, możemy na podstawie rysunku 69 otrzymać proste wzory, służące do obliczenia innych wartości przydatnych w projektowaniu i tyczeniu łuku kołowego z krzywymi przejściowymi.

Odcięta X_s środka koła krzywizny w punkcie P, a więc i fĘM tego okręgu, który tworzy dalszy odcinek trasy krzywoli-pwej, _

X_s = X — R sin x.    (65)

OdsunMlb H koła krzywizny od stycznej głównej

H = Y—R (1— cos t).    (66)

Rzędn^f_s środka koła krzywizny

Y_s = R+H = Y+iR cos t.    (67)

DługoBltf stycznej głównej (odległość od początku układu do fnktu p^p^iecia się normalnej ze styczną główną)

T = X+Y tg x.    (68)

Długa fccia się

w:

Krótki jej zel

|czna (odległość od początku układu do punktu prze-rcznej głównej ze styczną w punkcie P klotoidy)

Tp = X — Y ctg t.    ,    (69)

rczna (odcinek ód punktu P do punktu przecięcia tpzrią główrią)

(70)

(71)

(72)

lorm

‘ CO&S *

ne biegunowe dowolnego-punktu klotoidy fcłowy z sytrietrycznymi łukami klo-

Przeprowadzenie między dwiema przecinającymi się prostymi trasy krzywoliniowej, składającej się z dwóch odcinków klotoidy i łuku kołowego między nimi (rys. 70), jest tylko wtedy możliwe, gdy kąt zwrotu stycznych y^2r. W przeciwnym wypadku zabrakłoby miejsca na wstawkę łuku kołowego, a łuki klotoidy krzjHpfrałyby się. Z rysunku widać, że rozpatrując kąty przy punkcieB^ otrzymamy

ffe    Y = 2x+a,

i u jest tą częścią kąta środkowego, która przypada na łuk

^k»ry.

#

9 Pomiary specjalne cz. I    ^29