3582326841

Współrzędne geograficzne i prostokątne

Położenie dowolnego punktu na powierzchni elipsoidy może być wyznaczone za pomocą współrzędnych geograficznych lub prostych przestrzennych.

Jedna z płaszczyzn jest płaszczyzną równika, dwie pozostałe są prostopadłe do siebie płaszczyznami południków.

Przez każdy punkt na powierzchni elipsoidy możemy przeprowadzić południk, a następnie przyjmując jeden z południków jako początkowy, to jedną ze współrzędnych geograficznych - długość - A określamy jako kąt dwuścienny zawarty między płaszczyzną południka zerowego (początkowego) a płaszczyzną południka przechodzącego przez dany punkt

Długość geograficzna zmienia się od 0 do - 180 długości wschodniej i od 0 do + 180 długości zachodniej.

Druga współrzędna - szerokość ę - jest to kąt jaka normalna do powierzchni elipsoidy wystawiona w danym punkcie tworzy z płaszczyzną równika. Zmienia się od 0 do +90 na północ i od 0 do - 90 na południe.

Między współrzędnymi geograficznymi a prostokątnymi zachodzą związki - mając jedne współrzędne możemy obliczyć drugie.

Wzory:

■Jl-e² $m² q>

a( \-e²)smę

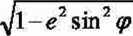
aco$<p

Szerokość geocentryczna i zredukowana

c

Szerokość geocentryczna - jest to kąt jaki tworzy promień wodzący OP z płaszczyzną równika.