740

'1

Tablica 44,7, Rozpiętości przełomowe

Strefa klimatycz na			Rozpiętość przełomowa cf^1 w				m dla s w	mm^1
	MPa		AFL-6			AFL-S	AFL-1,7
		35	70	120	240	525	30	70	95
	10	W)	! 9(6)	12	17	23	7(5)	8	10
	30	18(13)	27(19)	37	50	70	22(16}	25	29
	50	30(21)	44(32}	61	83	116	37(27}	42	49
	60	36(26)	53(39)	73	99	140	44(32)	50	59
	70	42(30)	62(45)	85	116	163	51(38)	53	69
	80	48(34)	71(52)	98	132	186	59(43)	67	78
i i ri	90	54(38)	80(58)	110	149	209	66(49)	75	88
	100	60(43)	89(65)	122	165	233	73(54)	83	98
	120	72(313	107(78)	146	198	279	88(65)	100	117
	140	-	-	-	-	-	102(75)	117	137
	180		-	-	-	-	132(97}	150	176
	200	-	-	-	-	-	146(103)	167	196
	10	4(3}	6(5)	9	13	18	5(4)	6	7
	30	13(9)	19(14}	27	38	54	16(12)	19	22
	50	21(14)	32(23)	45	63	90	27(20)	3L	37
	60	26(17)	39(28)	54	75	108	32(24)	37	44
ni	70	30(20)	43(33)	63	88	126	38(28)	43	52
	80	34(23)	52(37)	72	100	144	43(32)	50	59
	90	38(26)	58(42)	82	113	162	49(36)	56	66
	100	43(29)	65(47)	91	125	180	54(40)	62	74
	120 j	31(33)	78(56)	109	150	216	65(48)	75	88
	140	- r	-	-	-	-	75(55)	87	103
	180	- ;	-	-	-	-	97(71)	112	133
	200	f - r	-	-		-	108(79)	124	147

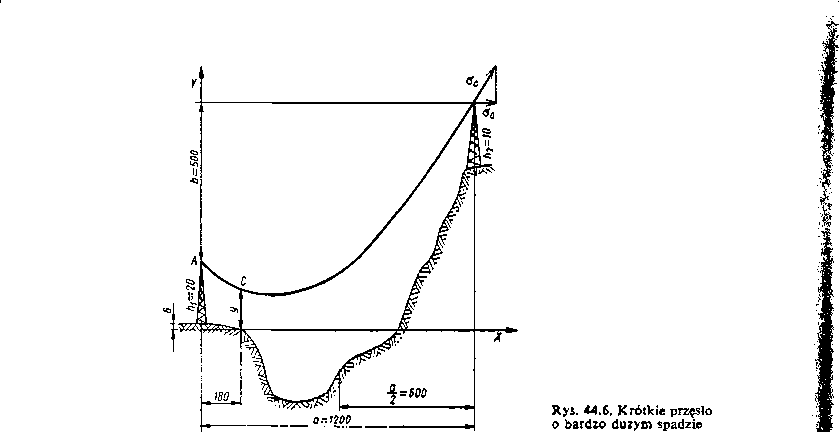
Rozpiętość przełomowa <j„ pozwala na określenie, w którym stanie „mró2” czy „sadź" powstają największe naprężenia, a więc który stan jest decydujący i będzie stanem wyjściowym w obliczeniach przęsła w warunkach normalnych (tabl. 44.7)

(44.29)

480*

2 2 ffp+t Sp

Gdy a < a_r warunkiem wyjściowym jest „mróz", a gdy a > a_t — „sądź”.

Temperatura krytyczna t_t jest to temperatura, w której zwis jest równy zwisowi w stanie „sadź”. Pozwala ona na określenie, w jakim stanie wystąpi największy zwis w przęśle

U =

1--*-ffp + s

(

)

-5

(44.30)

Dla t_k < + 40°C -* f_an = /+ 40, a dla h > +40*C -/_raa, =/,.

Rozpiętość krytyczna a_k jest to rozpiętość (w stanach „sadź” i „sadź katastrofalna”), przy której naprężenia osiągają dopuszczalne wartości. Pozwala ona na wybór jednego z tych stanów jako stanu wyjściowego.

Rozpiętość krytyczna jest z reguły bardzo duża i dotyczy przęseł rozwiązywanych metodą paraboliczno-lańcuchową (z wyjątkiem przewodów aluminiowych).

a_k = <Tj £7,*

J

24/? (u_łt — cr,)_

2 2 2 2 ttp + s2    p +■Ojfc

(44.31)

Gdy a < a_k warunkiem wyjściowym jest „sadź”, a gdy a > a_k — warunkiem wyjściowym jest „sadź katastrofalna”.

Naprężenia o, i <7,1 są naprężeniami poziomymi w wyższym punkcie zawieszenia przewodu (naprężenie poziome jest jednakowe w każdym punkcie krzywej zwisania), natomiast naprężenia o_e„ i (lub o<j_Im i ot™) — naprężeniami całkowitymi. Dlatego też wstawiane do wzoru (44.31) naprężenia er, i <r_di muszą być obliczone ite-racyjnie z naprężeń o_d„ i <r*„ za pomocą wzorów (44.11) lub (44.24)h-(44.25).

Zamiast wzoru (44.11) można wykorzystać wzór (44.18) — unikając w ten sposób obliczeń iteracyjnych,

Przykład 44.2.

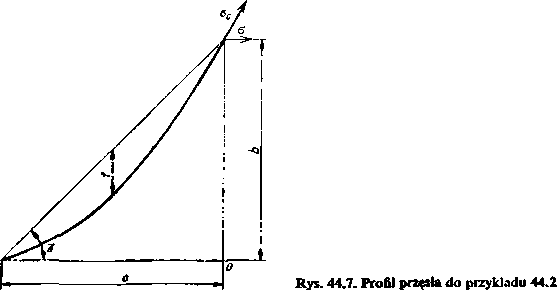
Dobrać naprężenie obliczeniowe i sprawdzić, czy odległość przewodów od krzyżowanej dróg¹ w przętle linii 220 kV pokazanym na rys. 44.7 spełnia wymagania normy. Linia przebiega w 1 strefie klimatycznej,

Dane: przewód AFL*8 525 mm³, ot — 19,4* I0^-6 1/°C, fi = 14*10-* MPa-^T, e„ = 32,93* 10^-3 N/fm-mm¹). p,+, = 52,35* 10-³ N/(m*mm^!).    = 71.S-10"³ M/(m-mm²),

1

W nawiasach podano a_p dla terenów ze zwiększoną sadzią, w pozostałych kolumnach a₉ dla tych terenów nie zmienia się.