Image078

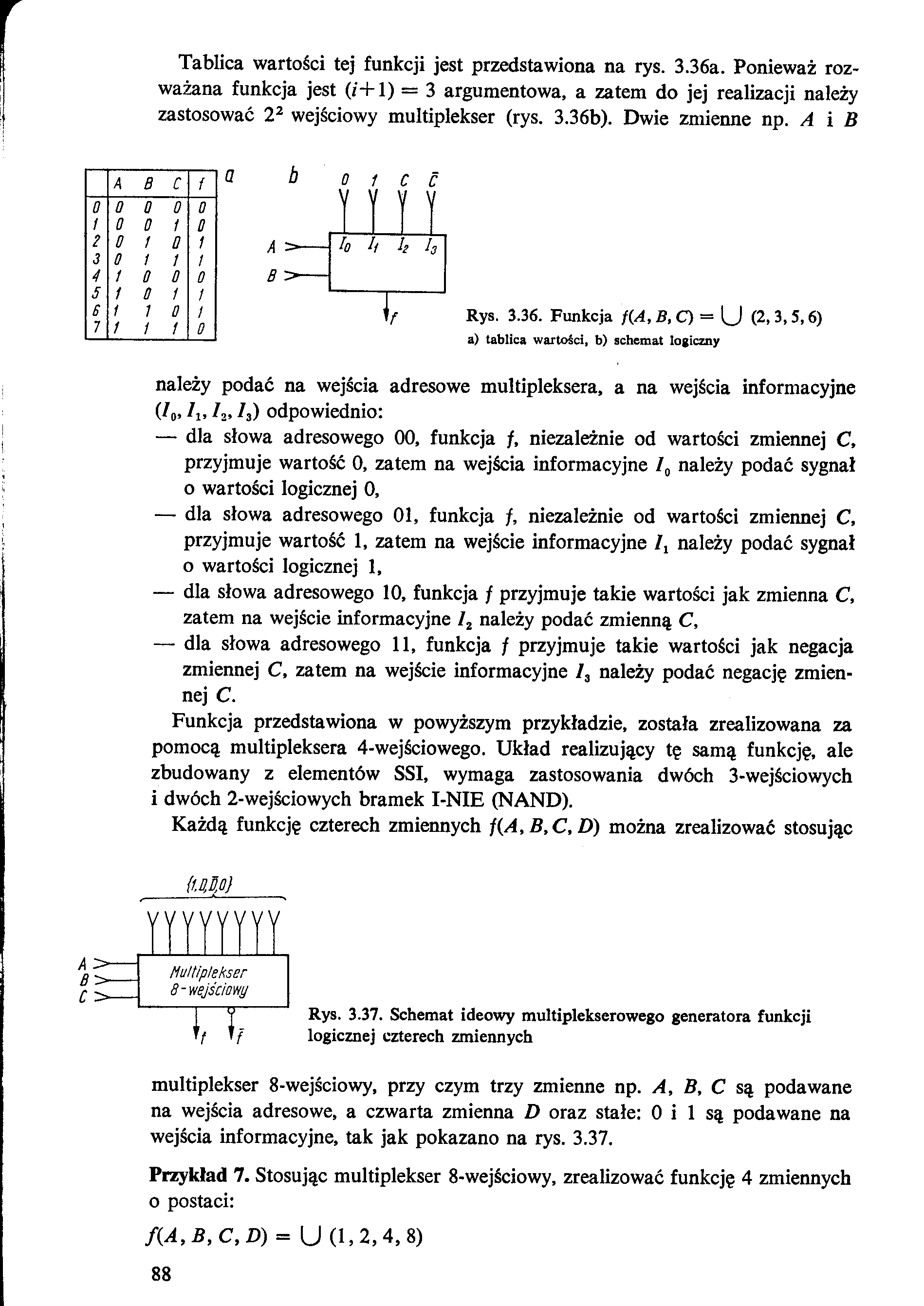
Tablica wartości tej funkcji jest przedstawiona na rys. 3.36a. Ponieważ rozważana funkcja jest (i+1) = 3 argumentowa, a zatem do jej realizacji należy zastosować 2² wejściowy multiplekser (rys. 3.36b). Dwie zmienne np. A i B

~A B CI I ⁰

b o 1 c ć

o o o o o 10 0 10 2 0 10 1

3    0    111

4    10 0 0

5    10    11

0 1 10 1 11110

A

B

1111

Rys. 3.36. Funkcja f(A,B,C) = U (2, 3,5,6)

a) tablica wartości, b) schemat logiczny

należy podać na wejścia adresowe multipleksera, a na wejścia informacyjne (7₀,7_ls 7₂, 7₃) odpowiednio:

—    dla słowa adresowego 00, funkcja /, niezależnie od wartości zmiennej C, przyjmuje wartość 0, zatem na wejścia informacyjne 7₀ należy podać sygnał o wartości logicznej 0,

—    dla słowa adresowego 01, funkcja /, niezależnie od wartości zmiennej C, przyjmuje wartość 1, zatem na wejście informacyjne l_x należy podać sygnał o wartości logicznej 1,

—    dla słowa adresowego 10, funkcja / przyjmuje takie wartości jak zmienna C, zatem na wejście informacyjne 7₂ należy podać zmienną C,

—    dla słowa adresowego 11, funkcja f przyjmuje takie wartości jak negacja zmiennej C, zatem na wejście informacyjne 7₃ należy podać negację zmiennej C.

Funkcja przedstawiona w powyższym przykładzie, została zrealizowana za pomocą multipleksera 4-wejściowego. Układ realizujący tę samą funkcję, ale zbudowany z elementów SSI, wymaga zastosowania dwóch 3-wejściowych i dwóch 2-wejściowych bramek I-NIE (NAND).

Każdą funkcję czterech zmiennych    D) można zrealizować stosując

Mo)

logicznej czterech zmiennych

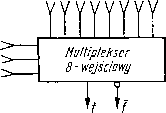
Rys. 3.37. Schemat ideowy multiplekserowego generatora funkcji

multiplekser 8-wejściowy, przy czym trzy zmienne np. A, B, C są podawane na wejścia adresowe, a czwarta zmienna D oraz stałe: 0 i 1 są podawane na wejścia informacyjne, tak jak pokazano na rys. 3.37.

Przykład 7. Stosując multiplekser 8-wejściowy, zrealizować funkcję 4 zmiennych o postaci:

f(A,B, C,D) = (J (1,2, 4, 8)

88