8 M1 MoniuszkoW DymekM ZAD84

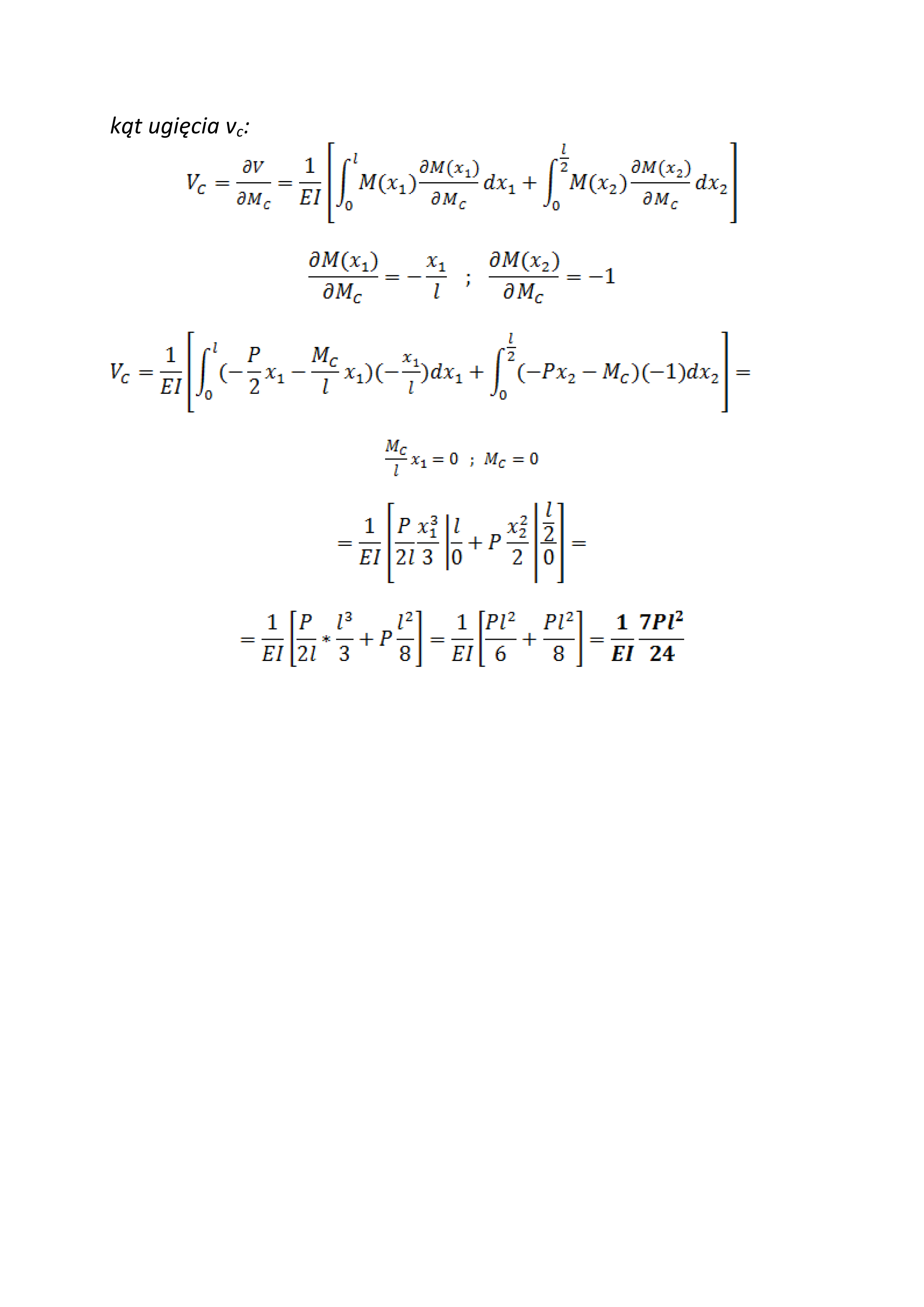
kqt ugięcia v_c:

V_c =

dv 1

dM_c El

dM(xA    f 2

jM(x₁)-^dx₁ + J M(x_: 2)

V_c =

		L
		dM^) xŁ	3M(x2)
		1	5MC
1	r* p	Mc x1	i r 2
£7	Jo^C"2^Xl	l *i)( f)^i +	(-Px ^0

= -1

M_c

~f^xi = ⁰ ’ ^Mc = ⁰

1

£7

P x\

YlY

dM(x_z)

dM_r

d,Xn

(-Px₂-M_cX-l)dx₂

i x|

- + P^f O 2

1

Yi

p    i²    1²

— *--b P —

21 3    8

1

£7

PI² PI² +

6 8

1 7 PI² Yl 24