8 M1 MoniuszkoW DymekM ZAD83

przedział: x_x E (0; l)

,    / P M_c\    P M_c

MOi) =    2 ““J*i ^{= _} 2^Xi_t^Xi

przedział: x₂ E (0;^)

M(x₂) = — Px₂ — M_c

ugięcie y_c:

dV dV₁ dV₂ ~^c dP dP dP

1

£7

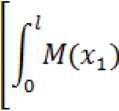
dM(x₁)

dP

i

dx₁ +

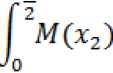
dM(x₂) dP

dx₂

dM(x_Ł) x₁ dM(x₂)

dP ⁼ ~T ' 3P

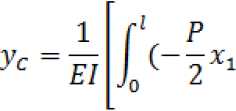
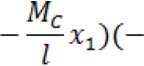
^xi

T

)dx₁ +

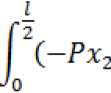
M_c)(-x₂)dx

2

1

£7

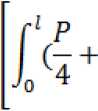
Mę

2Z

i

+

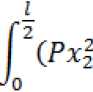
+ M_c%₂)dx_z =

i

¹ + M_C o ^L

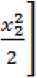
-+P^

O    3

Mr    X%

-rf = 0 ; M_c^ = 0 21 ^L 2

1

£7

PI³

⁽4 3^)+P

il

24

1 3Ff³

El 24

£7