906410ƒ2391546824916435898332451615342 o

spowodować wystąpienie zdarzenia wierzchołkowego. Przekroje są generowane zgodnie z zasadami algebry Boole'a. Istnieje wiele różnych algorytmów służących do generowania przekrojów.

Przekroje posiadają następujące właściwości:

1.    Przekroje niskiego rzÄ™du sÄ… przyczynÄ… wysokiej podatnoÅ›ci na uszkodzenia systemu. Przekrój pierwszego rzÄ™du jest zazwyczaj źródÅ‚em znacznego ryzyka.

2.    Przekroje wysokich rzÄ™dów w nieznaczny sposób wpÅ‚ywajÄ… na podatność systemu na uszkodzenia. Przekroje wysokich rzÄ™dów majÄ… tendencje do posiadania niewielkich prawdopodobieÅ„stw.

3.    Dla dużej ^:iczby przekroi analityk musi ocenić Å‚Ä…czne ryzyko zdarzenia wierzchoÅ‚kowego, ponieważ wszystkie przekroje dodane razem mogÄ… osiÄ…gać nieakceptowanÄ… wartość prawdopodobieÅ„stwa.

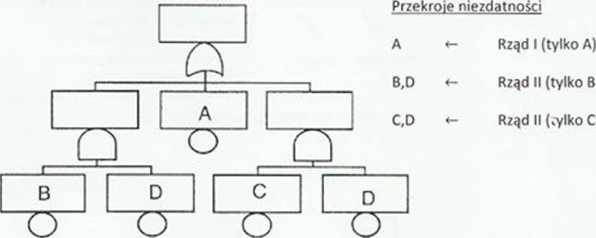
Rys. nr 1.8. Przekroje niezdatności przykładowego Drzewa Niezdatności.

1.5 Algorytm MOCUS

Jednym z najbardziej znanych algorytmów generowania przekrojów niezdatnoÅ›ci jest MOCUS (method of obtaining cut sets). ZostaÅ‚ on opracowany przez J. Fussell'a i W. Vesely'a. MOCUS bazuje na obserwacji, że bramki „I" zwiÄ™kszajÄ… liczbÄ™ elementów w przekroju, a bramki „Lub" zwiÄ™kszajÄ… liczbÄ™ przekrojów. Podstawowymi krokami algorytmu MOCUS sÄ…:

1.    Nazwanie oraz ponumerowanie wszystkich bramek i zdarzeÅ„.

2.    Umieszczenie nazwy bramki zajmujÄ…cej najwyższa pozycjÄ™ w pierwszym wierszu macierzy.

3.    ZastÄ…pieniu górnej bramki jej wejÅ›ciami w nastÄ™pujÄ…cy sposób:

a.    ZastÄ…pieniu bramki „f jej wejÅ›ciami, oddzielajÄ…c wejÅ›cia przecinkiem.

b.    ZastÄ…pieniu bramki „Lub" poprzez pionowe rozmieszczenie, tworzÄ…c nowÄ… liniÄ™ dla każdego wejÅ›cia.

4.    Kolejne podstawianie i zastÄ™powanie każdej bramki jej wejÅ›ciami, przesuwajÄ…c siÄ™ w dół Drzewa NiezdatnoÅ›ci.

5.    Gdy pozostanÄ… jedynie wejÅ›cia podstawowe, proces podstawiania jest zakoÅ„czony, a lista wszystkich przekrojów niezdatnoÅ›ci ustalona.

str. 11