CCF20091202019

wierzchniach proporcjonalnych do liczby przypadków. Jeśli wszystkie przedziały są równej długości, proporcjonalność powierzchni daje oczywiście te same wyniki, co proporcjonalność wysokości. Gdybyśmy przyjęli, że szerokość prostokąta wynosi 1, a jego wysokość równa jest proporcji przypadków w danym przedziale, to całkowite pole pod histogram równe będzie jedności. Czyli

1 (5/93)+1(17/93)+1 (39/93)+... +1(1/93) = 1

Omawiając krzywą normalną w rozdziale 7 stwierdzimy, że należy posługiwać się proporcjonalnością powierzchni, a nie wysokości i że często

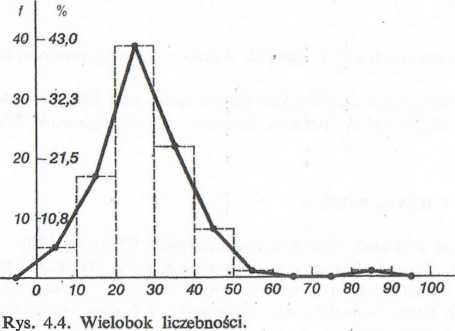
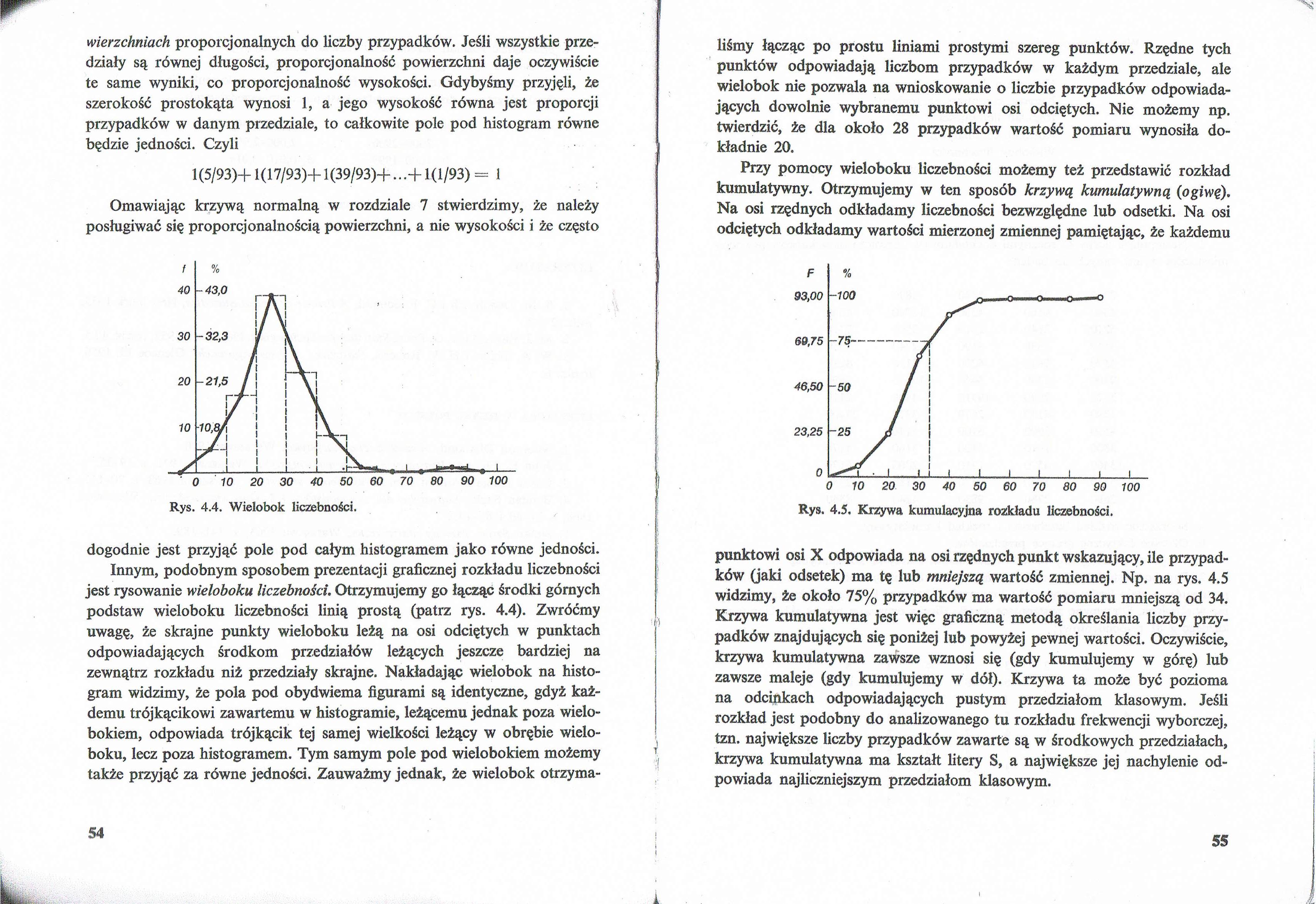
dogodnie jest przyjąć pole pod całym histogramem jako równe jedności.

Innym, podobnym sposobem prezentacji graficznej rozkładu liczebności jest rysowanie wieloboku liczebności. Otrzymujemy go łącząc środki górnych podstaw wieloboku liczebności linią prostą (patrz rys. 4.4). Zwróćmy uwagę, że skrajne punkty wieloboku leżą na osi odciętych w punktach odpowiadających środkom przedziałów leżących jeszcze bardziej na zewnątrz rozkładu niż przedziały skrajne. Nakładając wielobok na histogram widzimy, że pola pod obydwiema figurami są identyczne, gdyż każdemu trójkącikowi zawartemu w histogramie, leżącemu jednak poza wielo-bokiem, odpowiada trójkącik tej samej wielkości leżący w obrębie wieloboku, lecz poza histogramem. Tym samym pole pod wielobokiem możemy także przyjąć za równe jedności. Zauważmy jednak, że wielobok otrzymaliśmy łącząc po prostu liniami prostymi szereg punktów. Rzędne tych punktów odpowiadają liczbom przypadków w każdym przedziale, ale wielobok nie pozwala na wnioskowanie o liczbie przypadków odpowiadających dowolnie wybranemu punktowi osi odciętych. Nie możemy np. twierdzić, że dla około 28 przypadków wartość pomiaru wynosiła dokładnie 20.

Przy pomocy wieloboku liczebności możemy też przedstawić rozkład kumulatywny. Otrzymujemy w ten sposób krzywą kumulatywną (ogiwę). Na osi rzędnych odkładamy liczebności bezwzględne lub odsetki. Na osi odciętych odkładamy wartości mierzonej zmiennej pamiętając, że każdemu

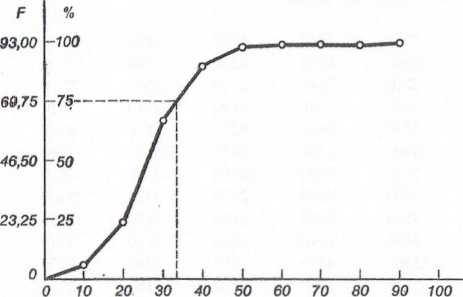
Rys. 4.5. Krzywa kumulacyjna rozkładu liczebności.

punktowi osi X odpowiada na osi rzędnych punkt wskazujący, ile przypadków (jaki odsetek) ma tę lub mniejszą wartość zmiennej. Np. na rys. 4.5 widzimy, że około 75% przypadków ma wartość pomiaru mniejszą od 34. Krzywa kumulatywna jest więc graficzną metodą określania liczby przypadków znajdujących się poniżej lub powyżej pewnej wartości. Oczywiście, krzywa kumulatywna zawsze wznosi się (gdy kumulujemy w górę) lub zawsze maleje (gdy kumulujemy w dół). Krzywa ta może być pozioma na odcinkach odpowiadających pustym przedziałom klasowym. Jeśli rozkład jest podobny do analizowanego tu rozkładu frekwencji wyborczej, tzn. największe liczby przypadków zawarte są w środkowych przedziałach, krzywa kumulatywna ma kształt litery S, a największe jej nachylenie odpowiada najliczniejszym przedziałom klasowym.

55