CCF20091202030

o największej liczbie przypadków, miernik ten można stosować nie tylko przy skalach porządkowych i interwałowych, lecz i nominalnych.

Istnieją też dwa inne mierniki tendencji centralnej, praktycznie niespotykane w literaturze socjologicznej. Są to średnia harmoniczna i średnia geometryczna. Określamy je wzorami:

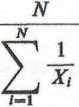
Średnia harmoniczna =

N

Średnia geometryczna = j/(Z₁)(J5T₂) ••• (Afjv)

W definicji średniej geometrycznej symbol N oznacza, że obliczamy pierwiastek iV-tego stopnia z iloczynu N pomiarów.

5.6. DECYLE, KWARTYLE I PERCENTYLE

Omawiając medianę wspomnieliśmy, że istnieją też inne mierniki pozycyjne, jak np. percentyle, które lokalizują pomiar większy niż pomiary stanowiące określoną proporcję wszystkich przypadków. Mierniki nie mierzą tendencji centralnej lub typowości, są jednak obliczane analogicznie do mediany. Zamiast więc znajdować wartość pomiaru, od którego dokładnie połowa pomiarów jest większa lub mniejsza, możemy szukać np. pierwszego kwartyla, czyli takiej liczby, od której 1/4 pomiarów jest mniejsza (lub równa). Podobnie, trzeci kwartyl jest liczbą, od której 3/4 pomiarów jest mniejsze (lub równe). Można też podzielić rozkład na 10 decyli podając liczby, od których 1/10, 2/10, 3/10, ..., 9/10 pomiarów jest mniejsze (lub równe). Bardziej znanym miernikiem są percentyle, które dzielą rozkład na 100 części. Tak więc, jeśli wyniki studenta w nauce znajdują się w 91-szym percentylu to oznacza to, że 91% studentów ma wyniki słabsze od niego.

Obliczanie decyli, kwartyli i percentyli jest analogiczne do obliczania mediany. Gdy dane są pogrupowane, określamy najpierw przedział, w którym dany miernik się znajduje. Znajdźmy więc np. pierwszy kwartyl dla danych z tabeli 5.4. Będzie to N/4-ty, czyli 47,25-ty pomiar. Z rozkładu kumulacyjnego widzimy, że pierwszy kwartyl leży w przedziale 3950-4950. Jest w nim 38 pomiarów, musimy więc znaleźć (47,25—43)/38 część prze-

działu. Wartość pierwszego kwartyla, Q_v wynosi więc

j

Q₁ = 3950+ —- 1000 = 3950+112 = 4062 doi.

Inne miary pozycyjne obliczamy podobnie. Zauważmy, że z definicji mediana jest równa drugiemu kwartylowi, piątemu decylowi i pięćdziesiątemu percentylowi. Chociaż decyle, kwartyle i percentyle rzadko spotyka się w literaturze socjologicznej, pojęcia te powinny być studentowi znane.

Ważniejsze pojęcia wprowadzone w niniejszym rozdziale

Decyl

Kwartyl

Mediana

Modalna wartość Percentyl Skośny rozkład Średnia

ZADANIA

1.    Podać średnią, medianę i wartość modalną następującej serii pomiarów: 26, 37, 43, 21, 58, 26, 33 , 45.

2.    Obliczyć średnią i medianę dla danych pogrupowanych w zadaniu 1, rozdz. 4 oraz w zad. 2, rozdz. 4.

3.    Obliczyć trzeci kwartyl, czwarty decyl i siedemdziesiąty pierwszy percentyl dla danych z zad. 1, rozdz. 4.

4.    Następujące (hipotetyczne) dane podają rozkład odsetka rodzin farmerskich w 60 powiatach. Obliczyć średnią i medianę.

Przedział, %	Liczebność
10-19	7 *
20-29	16 h
30-39	21 Z 3
f 40-49	12 li
50-59	4

60

5. Dla danych z poprzedniego zadania określić, jak zmieni się wartość średniej i mediany (zmniejszy się, zwiększy, pozostanie bez zmian), jeśli:

a.    Rozszerzymy ostatni przedział do 50-69, pozostawiając liczebności bez zmian;

b.    Wartość każdej granicy przedziału zwiększymy o 10 (tj. otrzymamy przedziały: 20-29, 30-39, itd.), pozostawiając liczebności bez zmian.

u.

77