DSCN5620

Obiic/ony całkowity fiadck cifaiwiifl pi - pz w pncwodae im na straty ciśnienia na pokonanie oporów wywołanych faraon < nym płynu i uporami miejscowymi w lym przewodzie. Z Bcmoulłiego wyniku, /c tylko w przypadku i/utermicawgo płynu prze/ poziomy przewód o stałym przekroju (d, *d₂\ spadek d-f'-'

•wnw ujcinna.. gayz «j «. W|, j wteay wiiftu.wny''sgSWK wiHDeOia mniejszy od strat ciśnienia na pokonanie oporów wywołanych tat^ wewnętrznym płynu i oporami miejscowymi w przewodzie.

Odpowiedź:

Całkowity spadek ciśnienia jest równy 2,4 • 10* Pa.

Przykład 1.6

W linii produkcyjnej do ogrzewania soku stosuje się wymiennik tyj_q I jura w rurze" o średnicy rury wewnętrznej 0,05 m i średnicy rury awrcię. nej 0.08 m. Sok o gęstości 1020 kg/m³ i lepkości 1,02'10' Pa s płyt* rurą centralną z prędkością I m/s. Stwierdzono, żc skierowanie soku przestrzeni między rurowej umożliwi trzykrotne skrócenie drogi osiąga* zadanej temperatury. Obliczyć, jak zmienią się straty ciśnienia przy tq zamianie, jeżeli wydajność linii musi być utrzymana na tym sanjm poziomie.

Dane:

£>0,08m

d-O^łSm a - I m/s

Szukane.

Rozwiązanie:

Dla pierwszego wariantu oblicza się liczbę Rer.

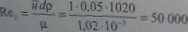
Średnica zasl^c/a przewodu o przekroju penckniowym wynoafc d_z = £>- d » 0*08—0,05 = 0.03 m Liczku Rej jest równa:

- 0.64 m/s

Re = “^.P _ 0.04 0,03-1020

1.02-10

10 200

Ruch jest również burzliwy, a odczytany z rysunku 12 wsp6tcrvnmk oporu przepływu dla rur chropowatych wynosi 0.033. Stna% cttoicma na pokonanie oporów przepływu oblicza się z równania

AT,

V

0.033

’ 10.64 >* -1020

0.03

2

16.6-I Pa