DYNAMIKA0006

DYNAMIKA

Ruch obrotowy bryły sztywnej

Bryłą sztywną nazywamy takie ciało, w którym odległości pomiędzy poszczególnymi elementami ciała nie zmieniają się, niezależnie od działających sił. Jeżeli bryła sztywna wiruje wokół osi obrotu, to piędkość kątowa to wszystkich jej elementów jest jednakowa.

Zmiana prędkości kątowej następuje pod wpływem momentów sil. Moment M siły /‘‘definiujemy:

- /•/•''sino    (2.25)

gdzie / jest odległością punktu przyłożenia siły od osi obrotu, a /‘ x ^B /•'sina jest składową siły prostopadłą do r (patrz rysunek).

Moment siły powoduje zmianę prędkości kątowej bryły sztywnej. Zgodnie z drugą zasadą dynamiki dla ruchu obrotowego:

&I4

M = Iz,    (2.26)

gdzie c - przyspieszenie kątowe bryły sztywnej (jednakowe dla wszystkich jej elementów), natomiast / jest momentem bezwładności bryły sztywnej, charateryzu-jącym rozkład jej masy względem osi obrotu :

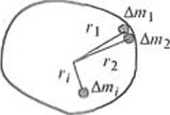
/ = A/wjrj + A/nj/ j ♦... + A/it/7 + + /W2.    (2.27)

gdzie A/n_I,A/n₂,.„Am_i ...£m_a - masy poszczególnych elementów ciała a r_[tr₂,...r_t ...r_B - ich odległości od osi obrotu (parrz rysunek).

Przykładowo obliczmy moment bezwładności cienkiej obręczy o masie m i promieniu R względem osi obrotu pokrywającej się z jej osią symetrii Odległości wszystkich elementów masy obręczy od osi obrotu są takie same i wynoszą R Stąd też moment bezwładności obręczy wynosi:

/ - mlł.    (2.28)

Moment bezwładności walca o masie m i promieniu R względem osi pokrywającej się z osią symetrii walca jest równy:

(2.29)

Momentem pędu ciała punktowego (ciała o małych rozmiarach) o masie Am,, poruszającego się w stałej odległości r od osi obrotu, nazywamy wielkość

K_i = /‘_/An;_/v_# ■ Am r^o)    (2.30)

Moment pędu bryły sztywnej jest sumą momentów pędu poszczególnych jej elementów: K = K\+Ki+ + +K„ Zgodnie z (2.30) i (2.27) wynosi on

(2 31)

50