ekologia06

Mhl II ni Mat lilwi

li

mmlii nlmiliMHilIr l*l» M nntnnaM

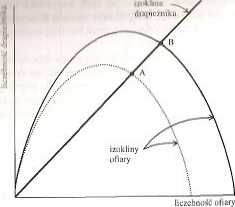
Myc. M.ft. Iiolcliliy drapieżnika i ollniy w klasycznym modelu Rosenzweiga i MncAnhura (a) oraz w mo-iłalu drnpirdnlOlwn obualronnlo zależnego od zagęszczenia (b). Dla populacji ofiary pokajane są dwie Imkllny: <lln rlcdllika banJ/iej i mniej produktywnego. Wzrost produktywności populacji ofiary w modelu kluiyouiyin powoduje tylko pizmunięcic punktu równowagi liczebności drapieżnika z A do B, w modelu di•ple*nklWl Obustronnie zależnego od zagęszczenia zmienia się liczebność równowagi obu ptunków (za: llaimlil l'JU|,/niieninne)

lin illn iliiiplożniku. juk i dla ofiary (ryc. 14.4). W pra-»*•) górnej ćwiartce olneiwuje sic spadek populacji Mównodiupieżnika. jak i ofiary, więc wektory skie-HwtiK kg w dół i do środka. W prawej dolnej fWaitcc liczebność populacji ofiar spada, zaś liczebno** populacji drapieżnika rośnie, więc wektory nliriiit do góry i do środka. Ćwiartka górna lewa Npiwlala sytuacji wzrostu liczebności populacji |Aliy | \|Miłku drapieżnika. Ćwiartka lewa dolna ■feniwiada spadkowi liczebności obydwu populacji, fp wygląda model oddziaływań drapieżnik-ofiara HiMtiir wny.i i Mac Arthura. Jest on banł/o użyteczni gdyż po/wula przedstawiać w sposób gra liczny ęłafciy /mian liczebności każdego z gatunków na • «ly układ drnptc/nik-ofiara.

Mm/ważmy leni/, sytuucję, w której jedynymczyn-iilkinii ograniczającym liczebność populacji drn-Me/nika jest pokarm (ofiary). IzokJina drapieżnika !■ >i wtedy pionowa i nic ma przegięcia (ryc. I4.5a). j iilif układ Jut irwaly. a wytracony z punktu równo* Wilgi wyku/uje oscy facjo /bieżne, powracając do li>||ii |itiiikiii. Uu/.wnżmy len iiuln pr/.ypndek, lec/

t/vjml|my, że diuplożnlk |eiil lunrl/.ioj efektywny, '/uml tloklywnośol drapieżnika tr/aiuc/n, fc może on utrzymać się przy mniejszej liczebności populacji ofiar, na naszym wykresie izoklina drapieżnika przesunięta więc zostanie w lewo (ryc. 14.5b). Jeśli izoklina drapieżnika przecina izoklinę ofiary na lewo od jej punktu szczytowego, układ nie osiąga stanu równowagi. lecz bezustannie oscyluje wokół hipotetycznego punktu równowagi. Im hardziej punkt (en jest oddalony od szczytu izokliny ofiary, tym większa jest amplituda oscylacji wokół niego.

Modd oddziaływań drapieżnik-ofiara Rosen-zweiga-MacArthura dopuszcza więc wiele różnorodnych przebiegów dynamiki liczebności: od stanu równowagi aż po silne oscylacje. Model len może również dostarczać odpowiedzi na wiele pytań, takich jak na przykład, jaki będzie skutek zmniejszenia się liczebności populacji ofiar? Model może stanowić również dobry punki wyjścia do prób głębszego zrozumienia rzeczywistych zależności.

Omawiane tu modele oddziaływań drapieżnik-ofiira zawierają w sobie wiele założeń upraszczających istniejącą rzeczywistość. Zakłada się w nich więc hontogenność środowiska, w którym bruk jest /.różnicowaniu nictlliNk. u ofiara nio ma kryjówek. Modele imuli/ojii układy »lclmll\|l|t)i> się /. jednego