PICT6492

■V

zamieszkania i płcią badanych a terminem ukończenia studiów. Dane te prezentuje tabela 22.

Można na podstawie danych zawartych w tabeli stwierdzić, że między analizowanymi cechami występuje zależność o różnym nasileniu. Zależność pomiędzy płcią a terminem ukończenia studiów jest silniejsza, niż. pomiędzy miejscem zamieszkania a terminem ukończenia studiów.

Tabela 22. Miejsce zamieszkani* i płeć studentów a termin ukończenia studiów

Miejsce zamieszkania	Studia ukończone
	w terminie	po terminie
Ogółem	100,0	100.0
Miasto	45.0	55.0
Wieś	55.0	45.0
Pleć	X	X
Ogółem	100.0	100,0
Mężczyźni	00.0	40.0
Kobiety	40.0	60.0

Przedstawiony rozkład procentowy informuje wprawdzie, która zależność jest silniejsza, lecz nic informuje o sile tych zależności. Aby ją określić należy wykorzystać współczynniki omówione w dalszych częściach pracy.

Współczynnik korelacji cech jakościowych Pcarsona nadaje się do ustalenia poziomu zależności między cechami jakościowymi w tabelach dy-chotoniicznych. tj. w tabelach, z których każda cecha ma dwa warianty. Można go stosować także, gdy cechy są ilościowe. Obliczenie współczynnika cech jakościowych wymaga, aby obie zmienne „X” i „Y" były ciągłe, miały rozkład normalny a zależność między nimi była liniowa. Cechy te muszą być tak podzielone, aby każda obserwacja była jednoznacznie podporządkowana wariantowi danej cechy: np. cecha „płeć” ma dwa warianty: mężczyźni (.v,) i kobiety (a\) zaś cecha „uczniowie uspołecznieni", ma także dwa warianty: aktywni (Aj) i bierni (x₂ ). Wartość współczynnika korelacji cech jakościowych waha się w granicach od +1 do 1. Ogólny schemat tabeli cztcropolowcj zamieszczono poniżej

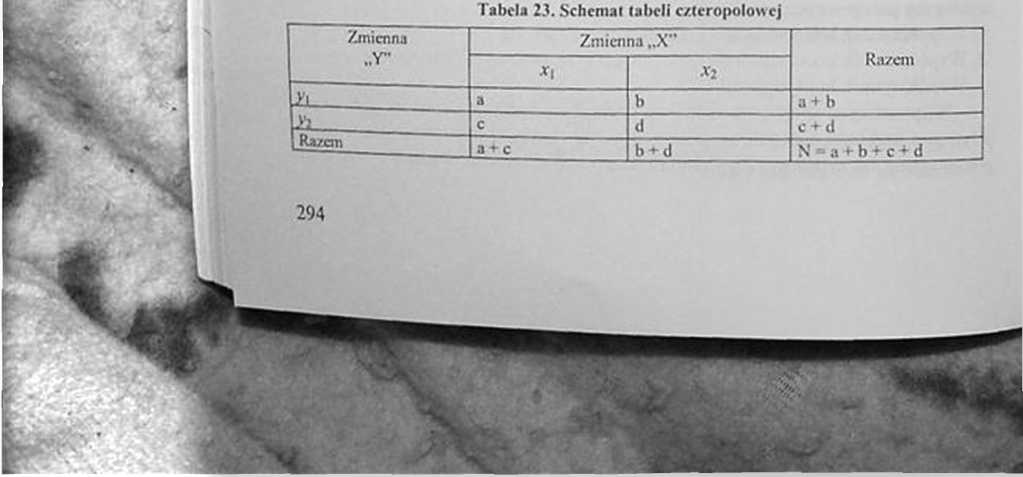
Zmienne w tabeli mogą być tak rozmieszczone, że wartości    mogą

nie występować, np. wśród uczniów uspołecznionych (X), może nie być uczniów biernych (,v.), a wśród uczniów wywodzących się z środowiska wiejskiego (Y), może nie być uczniów interesujących się np. muzyką (y₂). Ponieważ obserwacja „d" (krzyżowanie .v, i y₂) może nic mieć cechy „X" i nic mieć cechy „Y”, wówczas współczynnik nic ma zastosowania.

Współczynnik korelacji cech jakościowych Pearsona obliczamy wg wzoru:

ad-be

r. -    ..    -    »    —t~ - r-

•Jfa + b)(a * c)(h + d)(c+d)

r. współczynnik korelacji cech jakościowych Pearsona.

Przykład. W wyniku badania aktywności społecznej 90 uczniów klas II i 111 gimnazjum ustalono, że 64 uczniów posiada postawy kwalifikujące ich do określenia jako uczniów „aktywnych” a 26 jako „biernych". Spośród 64 aktywnych uczniów', 33 uzyskiwało oceny powyżej średniej a 31 poniżej średniej ocen w klasie. Wśród uczniów biernych S osób posiadało oceny powyżej średniej a 1S poniżej średniej w klasie. Rozmieszczenie danych dotyczących wyników nauczania oraz aktywności społecznej badanych uczniów prezentuje tabela 24.

Tabela 24. Uczniowie wg uspołecznienia i wyników nauczania

Uspołecznienie	Wyniki nauczania		{Won
uczniów	Poniżej średniej	Powyżej średniej
Aktywni	31	33	64
Bierni	1S	S	26
Ogółem	49	41	90

>3«1S)-(31»S) _ 346 /ó4-26-41 • 49 IS2S

Współczynnik korelacji cech jakościowych wskazuje na słabą zależność między zmiennymi a cechami uczniów. Z obliczeń wynika, że uspołecznienie uczniów- nie ma istotnego wpływu na osiągane przez nich wyniki w nauczaniu. Jednak z tabeli można odczytać, że uczniowie bardziej aktywni, otrzymują częściej oceny powyżej średnich niż uczniowie bierni.

Współzależność cech można obliczyć tak/.c za pomocą współczynnika kontyngcncji Współczynnik ten służy do określenia siły związku pomiędzy cechami jakościowymi. Opiera się na statystyce Chi kwadrat (C/r).

Stosujemy go zarówno do tabel czteropolowych, tj. takich, w których dwie cechy posiadają po dwa warianty, jak i tabel o większej liczbie pól. Współczynnik kontyngencji „C” obliczamy wg następującego w^zoru (G. Klauss, H. Ebner 1972, s. 30]:

295